Cet article n’est pas un article sur l’histoire des sciences ou de la pensée statistique et n’a aucune prétention d’académisme ou d’objectivité. Il est le fruit d’une rencontre entre Matthieu, informaticien expert en machine learning et Michel, statisticien de formation. Ils se sont retrouvés chez OCTO par la pratique du même métier, data scientist. En travaillant ensemble, ils ont compris qu’ils avaient développé, du fait de leurs cursus respectifs, des façons très différentes d’aborder l’analyse de données. Curieux d’échanger leurs savoirs, ils se sont amusés à mettre en regard leurs domaines scientifiques respectifs, ce qui les a amené à comprendre à quel point ils étaient étroitement liés.
Cet article propose donc de partager cette vision croisée sur la data science telle qu’ils la pratiquent sur le terrain dans le quotidien de consultant. Pour cela, une approche chronologique est proposée. Cet article montre en effet comment des préoccupations scientifiques et philosophiques distinctes se sont progressivement retrouvées pour aboutir à la data science d'aujourd’hui, et peut-être à l’intelligence artificielle de demain.
A cet effet, le plan suivant est proposé. Tout d'abord, nous remonterons loin dans le temps, en montrant comment la statistique est devenue un outil indispensable à la création de connaissances humaines et en expliquant comment l'homme, au travers d'un rêve de philosophe, s'est posé la question de l'automatisation de son processus de production de connaissances. Dans une deuxième partie, nous expliciterons comment ce rêve de philosophe est devenu un projet d'ingénieur, qui a donné naissance à l'informatique et aux premières intelligences artificielles. La statistique en sera profondément bouleversée. Ceci nous amènera à la troisième et dernière partie, qui donnera quelques éclairages sur la data science contemporaine, conséquence des bouleversements évoqués.
Prêt à remonter le temps avec vos deux data guide ?
L’analyse de données s’est fortement développée avec la pratique scientifique. Pour justifier ce propos, commençons par proposer une définition de la science. Elle peut être vue comme :
Du latin scientia, “connaissance”, la science est ce que l’on sait pour l’avoir appris, ce que l’on tient pour vrai au sens large, l’ensemble de connaissances, d’études d’une valeur universelle, caractérisées par un objet (domaine) et une méthode déterminés, et fondées sur des relations objectives vérifiables. (Source Wikipedia)
Pour développer des connaissances relatives à un domaine, des procédés d’apprentissage sont nécessaires. En effet, de façon générale, on peut définir l’apprentissage comme
un ensemble de mécanismes menant à l’acquisition de savoir-faire, de savoirs ou de connaissances (Source Wikipedia)
De nombreux articles montrent comment les données contribuent à la création de connaissances, s’appuyant généralement sur la hiérarchie “données - informations - connaissances” proposée par Ackoff (Ackoff 1989).
Plus précisément, c’est l’exploitation de données par le développement d’outils statistiques qui s’est rapidement imposée comme un puissant outil de création de connaissances pour l’homme. C’est ce qu’explique Desrosières dans son ouvrage magistral (Desrosières 2010, en mettant en évidence les champs scientifiques qui ont contribué aux premiers succès de la statistique. En lisant cet ouvrage, on comprend à quel point l’analyse de données s’ancre loin dans l’histoire de l’homme, lui permettant de développer des connaissances nouvelles. C’est ce qu’illustre le paragraphe suivant.
Dans ce qu’on appellerait aujourd’hui les sciences humaines (sciences politiques, sociologie, géographie…), l’analyse de données a rapidement trouvé une place de choix, afin de dénombrer et trouver des modes efficaces de représentation de la taille, la richesse, la puissance, d’une communauté humaine (un Etat ou une région, par exemple) (Desrosières 2010, Adler 2013). C’est d’ailleurs là que l’on trouve l’origine du mot “statistiques”, issu du latin status, “relatif à l’état”. Pour l’histoire, même si l’on en parle déjà dans la Bible lorsque Moïse et Aaron recensent tous les hommes d’Israël de vingt ans ou plus aptes à se battre, la première trace physique de ces pratiques de dénombrement remonte à 3000 ans avant JC, sous la forme de tablettes d’argile sumériennes comptant hommes et biens. Une approche plus systématique s’est surtout développée à partir du 18ème siècle, selon deux écoles :
Il en va de même pour les sciences de la nature (astronomie, physique…), où l’on a pris conscience que la compréhension des phénomènes de la nature passe par le recueil et l’analyse de données. L’astronomie, par exemple, est étroitement liée à l’histoire de l’analyse de données (Desrosières 2010, Adler 2013 ou voir aussi (Source Science et Avenir) ). Johannes Kepler a remis en cause le système ptoléméen en se basant sur des mesures réalisées par Tycho Brahe pendant des milliers heures d’observation du ciel. Carl Friedrich Gauss a prédit la trajectoire et retrouvé l’astéroïde perdue Cérès sur la base des observations de l’astronome Piazzi en élaborant à peu près en même temps que Legendre une méthode encore reine aujourd’hui en statistiques : les moindres carrés. Elle permet de comparer des données expérimentales, généralement entachées d’erreurs de mesure, à un modèle mathématique censé décrire ces données.
Ces premières approches se sont progressivement enrichies des développements issus d’un autre domaine : la probabilité. Née dans les salles de jeux plutôt que par l’observation respectable des étoiles, elle a néanmoins posé des concepts puissants qui ont profondément influencé toutes les disciplines scientifiques. Par exemple, le problème de l’extrapolation d’un petit nombre d’observations à l’ensemble d’une population va y trouver un cadre formel, très utile pour les techniques de sondage. Autre exemple, la méthode des moindres carrés déjà évoquée à été enrichie d’une interprétation probabiliste, qui en fait un puissant outil de modélisation et de prévision en contexte d’incertitude. Pour une vue historique plus complète de cette évolution des statistiques, se référer aux références suivantes : (Desrosières 2010, Droesbeke 1990, Adler 2013).
Dès la fin du 19ème, l’approche par la donnée s’est rapidement imposée avec l’essor de l’empirisme et de la science expérimentale. En sciences politiques, la statistique anglaise strictement quantitative est devenue prépondérante, au détriment de la statistique allemande. L’exploitation méthodique des données dans les sciences physiques s’est tant généralisée que la statistique est devenue la « grammaire de la science », titre d’un ouvrage du célèbre statisticien Karl Pearson (Pearson 1912). On pourrait multiplier les illustrations, pas une science ne semble s’être construite sans un recours massif à l’analyse de données : biologie, sociologie, économie...
Ces succès ont conduit à ce que tous ces travaux relatifs à l’étude des données s’organisent autour d’une science à part entière : en 1919 est créée la première chaire de statistique à l’université de Londres (Arribas 2004). Schématiquement, cette science s’articule aujourd’hui encore autour de deux grandes disciplines : les statistiques descriptives et exploratoires et les statistiques inférentielles et confirmatoires (Lebart 2006) :
Fasciné par la capacité de l’homme à produire des connaissances, et à développer des méthodes et outils lui permettant de comprendre son monde, l’homme va peu à peu se demander si cette faculté peut elle-même être comprise, systématisée et, pourquoi pas, déshumanisée. C’est ainsi que va naître le rêve du philosophe, sous l’impulsion de Leibniz : modéliser les mécanismes d’apprentissage. Pour cela, deux verrous devraient être levés : formaliser un langage universel du raisonnement (la lingua philosophica) et manipuler automatiquement les idées via un processus mécanique (le calculus raciocinator).
Dans son ouvrage De Arte combinatoria publié en 1666 (Leibniz 1666), Leibniz propose l’idée d’un “alphabet de la pensée humaine” avec lequel toute idée complexe pourrait être décomposée en idées plus simples jusqu’à aboutir à une combinaison d’idées axiomatiques. Il discute ainsi de la possibilité d’un langage symbolique qu’il nomme “la caractéristique universelle” (characteristica universalis ou lingua philosophica) qui permettrait de formaliser des raisonnements comme de simples calculs mécanisables.
Leibniz considérait ce concept comme une pièce maîtresse de son oeuvre. En voici un résumé présenté dans une lettre au duc Johann Friedrich (Martin 1966) :
Par là toutes les notions composées de l’univers entier sont réduites en peu de notions simples qui en sont comme l’alphabet et, inversement, il est possible de trouver avec le temps, par une méthode ordonnée, par une combinaison de cet alphabet, toutes les choses avec tous leurs théorèmes et ce qu’on n’en pourra jamais trouver. Je considère que cette invention, pour autant que si Dieu le veut, elle est réalisée, est comme mère de toutes les inventions.
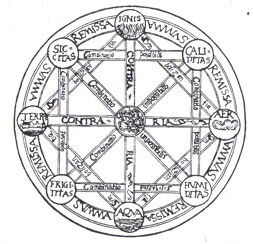
Ainsi, comme dans l’image de couverture de sa thèse “De Arte combinatoria”, ou les choses matérielles sont formées des éléments terre, air, eau et feu, des idées axiomatiques pourraient être combinées jusqu’à former les pensées philosophiques les plus complexes.
Au delà de la formalisation de raisonnements complexes, une mécanique permettrait de les résoudre voire d’explorer des modes de raisonnements nouveaux et ainsi d’étendre les capacités humaines.
Leibniz serait allé jusqu’à déclarer :
Alors, il ne sera plus besoin entre deux philosophes de discussions plus longues qu’entre deux mathématiciens, puisqu’il suffira qu’ils saisissent leur plume, qu’ils s’asseyent à leur table de calcul (en faisant appel, s’ils le souhaitent, à un ami) et qu’ils se disent l’un à l’autre : “Calculons !"
Leibniz est d’abord confiant en son approche (von Leibniz 1969) :
Je pense que quelques hommes bien choisis pourraient finaliser l’approche en 5 ans
Mais il perd peu à peu l’espoir de pouvoir formaliser ce langage. Ces travaux, bien que restés à un niveau philosophique, ont inspiré bien des philosophes et des mathématiciens lors des siècles à venir.
Une théorie va matérialiser les travaux de Leibniz et déclencher de nombreuses innovations dans les années à venir, dont les premiers circuits logiques. Celle-ci est due à un jeune autodidacte anglais, George Boole, né le 2 novembre 1815 à Lincoln (Royaumes-Unis).
Issu d’une famille pauvre, George Boole est doté de capacités intellectuelles exceptionnelles, il travaille dès 16 ans en tant qu’enseignant pour subvenir aux besoins de sa famille. Par la suite, il se plonge dans l’étude des mathématiques et s’impose comme une personnalité importante de cette science.
En 1854 dans son livre “An investigation of the laws of thought, on which are founded the Mathematical of logic and Probability”, George Boole s’appuie considérablement sur les concepts de Leibniz.
Le but de ce traité est d’étudier les lois fondamentales des opérations de l’esprit par lesquelles s’effectue le raisonnement ; de les exprimer dans le langage symbolique d’un calcul, puis sur un tel fondement, d’établir la science de la logique et de constituer sa méthode puis de faire de cette méthode elle-même la base d’une méthode générale que l’on puisse appliquer à la théorie mathématique des probabilités ; et enfin, de dégager des différents éléments de vérité qui seront apparus au cours de ces enquêtes des conjectures probables concernant la nature et la constitution de l’esprit humain. (Boole 1854)
La logique traditionnelle concerne les principes généraux du raisonnement avec comme outil le langage naturel. Boole propose de construire une logique symbolique via des outils mathématiques.
The laws we have to examine are the laws of one of the most important of our mental faculties. The mathematics we have to construct are the mathematics of the human intellect.
Dans son formalisme, Boole introduit une notion de symbole afin de minimiser l’ambiguïté du langage naturel et pouvoir manipuler plus facilement des concepts. Ces symboles représentent des classes qui désignent des groupement d’objets arbitraires. Par exemple le symbole X représentant la classe des boules blanches dans une urne et le symbole Y la classe des boules noires. Dans son ouvrage Boole introduit également un ensemble d’opérateurs logiques (NON, ET, OU) qui permettent de manipuler cet algèbre.
Boole a réussi là où Leibniz a échoué : la manipulation par le calcul de représentations de concepts abstraits issus du raisonnement humain. Cette théorie était très novatrice, car ces avancées de George Boole ont été développées indépendamment des théories de Leibniz, dont la majorité des textes logiques ont été découverts et publiés au début du 20ème siècle par Couturat (Serfati 2000). Ainsi la veuve de George Boole, Mary Everest Boole, écrivit que son mari ayant été informé des anticipations de Leibniz sur sa propre théorie ressenti (Laita 1976) :
as if Leibnitz had come and shaken hands with him across the centuries
Ces nouveaux développements sur la logique ont inspiré de nombreux mathématiciens mais c’est David Hilbert qui va réellement institutionnaliser la logique et l’ancrer comme discipline à part entière des mathématiques modernes (Gasser 2000).
Il s’inspire de la logique symbolique pour ses travaux sur la cohérence des mathématiques, travaux qu’il intégrera dans les célèbres “23 problèmes de Hilbert”(Source Wikipedia). En particulier, le second et le dixième problème de Hilbert nous intéressent, car ils feront entrer en jeu des grands noms de l’histoire de l’intelligence artificielle.
Le premier problème avait pour objectif de
Démontrer la consistance des axiomes de l’arithmétique.
Les mathématiques sont construites à partir d’axiomes. Par exemple, en géométrie euclidienne, “Un segment de droite peut être tracé en joignant deux points quelconques distincts” (Source Wikipedia). On considère qu’une théorie est cohérente (ou par anglicisme “consistante”) si aucune formule P telle que P et sa négation P soient toutes deux prouvables à partir des axiomes de la théorie (Source Wikipedia). Hilbert avait l’intuition que les axiomes de l’arithmétique étaient consistants et qu’ils ne permettaient pas de démontrer à la fois un énoncé et sa négation.
Cette question restera posée pendant 20 ans. En 1931, Kurt Gödel dans son article « Sur les propositions formellement indécidables des Principia Mathematica et des systèmes apparentés » expose ses “théorèmes d’incomplétude” et apporte une réponse formelle et négative (Source Wikipedia).
Le dixième problème avait pour objectif de :
Trouver un algorithme déterminant si une équation diophantienne a des solutions.
Ce problème est à la source d’une grande question du début du 20ème siècle : la question de la décidabilité.
Tout raisonnement est-il décidable, est-il possible de formuler une langue formelle unique permettant d’exprimer toutes les vérités et démonstrations, ne serait-ce que dans le domaine logique et mathématique ?
En s’inspirant des travaux de Gödel, Alonzo Church et Alan Turing ont prouvé dans des publications indépendantes qu’une solution générale est impossible. Pour prouver ce résultat, il fallait définir ce qu’était une fonction calculable. Cette définition est apparue avec le lambda-calcul de Church et les célèbres machines de Turing.

En proposant la machine de Turing, Turing défini une description mathématique d’un processus simple capable de faire n’importe quel calcul. Il prouve en particulier que certaines catégories de problèmes ne peuvent être résolues avec la machine de Turing répondant ainsi à la question de la décidabilité.
Très rapidement, Turing s’intéresse non-pas à la machine de Turing comme abstraction mathématique, mais voit son potentiel en terme d’utilisation réelle. Il prouve ainsi que tout problème décidable est mécanisable avec sa machine de Turing. La voie est ouverte vers la mécanisation du travail des computers humains.
Toutefois, Turing voit déjà plus loin, pensant que sa machine offre un potentiel illimité, et qu’elle pourra un jour se substituer à l’homme même pour des tâches non répétitives et créatives. Il ira jusqu'à proposer le célèbre "Test de Turing" afin de mesurer la capacité d'une machine à avoir un comportement réellement intelligent.
Shannon et sa souris électromécanique (Source Wikipédia)
En 1938, Claude Shannon transpose dans la réalité l'algèbre de Boole en prouvant que cet outil permet de simplifier la conception des automates électromécaniques qui sont à la base des communications téléphoniques à l'époque (basés sur des assemblages de relais électriques).
Il décrit également l'utilisation de ces relais pour résoudre des problèmes décrits dans l'algèbre de Boole.
Shannon a également créée une des premières expériences de résolution automatique d'un problème d'intelligence artificielle avec sa souris mécanique Theseus qui devait pouvoir retrouver son chemin dans un nouveau parcours sans programmation et enregistrer ses expériences.
 Le Harvard Mark I (Source Wikipédia)
Le Harvard Mark I (Source Wikipédia)
L'idée d'utiliser les relais comme portes logiques a inspiré la conception des premiers ordinateurs et des circuits électroniques. En moins de 10 ans de nombreuses avancées vont être réalisées jusqu'à la réalisation du célèbre "Harvard Mark I", en se basant sur les travaux d'Howard Aiken, le premier calculateur à usage généraliste.
Le Mark I restait une machine électro-mécanique qui ne disposait pas de possibilités de programmation. Une de ses premières utilisation a été comme support dans la conception de la bombe atomique.
A partir de 1950, les premiers ordinateurs sortent du domaine militaire et s'ouvrent à d'autres utilisations. Apparaissent également les premiers langages de programmation généralistes. Ces nouveaux outils nous permettent d'entrer dans une mécanisation des différentes abstractions humaines (logique, statistiques, etc). Le rêve du philosophe est en partie résolu sur la lingua philosophica et devient un problème d’ingénierie. Toute abstraction humaine est maintenant représentable et manipulable par l’intermédiaire de systèmes informatiques, qui permettent de stocker de l’information et la manipuler. Dans le cadre de la loi de Moore, ces capacités de stockage et de manipulation n’auront cesse de s’accroître.
Cette première étape de la mécanisation du rêve du philosophe se limite encore à l’automatisation de raisonnements déterministes. Le calculus raciocinator de Leibniz, la capacité de manipuler les abstractions de manière automatique avec un raisonnement automatique, n’est encore que de la science-fiction.
Cependant dès les années 1950, la recherche en informatique lance les premières initiatives à grande échelle pour aller au delà d'une programmation déterministe. L'objectif est maintenant de reproduire des processus humain de raisonnement et d'apprentissage.
Un événement clé de cette période est la célèbre conférence de Darmouth "Dartmouth Summer Research Project on Artificial Intelligence". Organisée par John McCarthy, Marvin Minsky, Nathaniel Rochester et Claude Shannon, il s'agit du premier événement scientifique ou le terme "intelligence artificielle" est utilisé.
Ses objectifs sont ambitieux (Source Wikipedia) :
We propose that a 2 month, 10 man study of artificial intelligence be carried out during the summer of 1956 at Dartmouth College in Hanover, New Hampshire. The study is to proceed on the basis of the conjecture that every aspect of learning or any other feature of intelligence can in principle be so precisely described that a machine can be made to simulate it. An attempt will be made to find how to make machines use language, form abstractions and concepts, solve kinds of problems now reserved for humans, and improve themselves. We think that a significant advance can be made in one or more of these problems if a carefully selected group of scientists work on it together for a summer.
Au cours de cette conférence, Newell et Simon présentent un programme intitulé "Logic Theorist" qui permettra par la suite de prouver automatiquement 38 des 52 théorèmes du chapitre 2 des Principia Mathematica (Source Wikipedia). Certaines de ces démonstrations faisaient preuve d'élégance et d'originalité démontrant que des raisonnements symboliques complexes pouvaient être automatisés.
Cette démonstration constituait une des premières preuve que des tâches autrefois considérées comme créatives et complexes pouvaient être reproduites mécaniquement.
Il s'ensuit un âge d'or où de nombreux programmes d'expérimentation sont financés, en particulier par la défense américaine, autour du raisonnement automatique et du traitement du langage naturel.
Le sentiment général est l'optimisme tant les avancées semblent importantes (Source Wikipedia) :
Cependant la majorité des approches de cette époque suivent le modèle du "computationnalisme", i.e. la représentation du raisonnement humain comme un système de traitement de l'information, la pensée étant réduite à un calcul et à l'application d'un système de règles. Cette modélisation permettait de nombreuses expérimentations autour du raisonnement automatique, mais était vite confrontée aux limites du modèle en terme d'adaptation à de nouvelles données ou à des nouveaux contextes.
 Le premier perceptron était implémenté physiquement - Mark I Perceptron machine (Source Wikipédia)
Le premier perceptron était implémenté physiquement - Mark I Perceptron machine (Source Wikipédia)
Une approche alternative, le modèle "connexionniste" montre également des résultats intéressants avec le célèbre "perceptron". Créé en 1957 par Frank Rosenblatt, le perceptron s'inspire du modèle biologique des neurones humains pour représenter l'apprentissage et le traitement de l'information. Avec ce modèle, des premières expérimentations autour de la reconnaissance des formes sont lancées.
Cette approche donnera naissance par la suite aux réseaux de neurones plus complexes tels que les "perceptrons multi-couches" et bien sûr aux récentes avancées autour des modèles de "Deep learning".
Cet engouement pour l'intelligence artificielle va connaître un premier "coup de froid" dès 1974 où l'absence de résultats pratiques et la faible puissance des machines limitent l'application de ces techniques.
Une troisième approche va apparaître à la fin des années 60 : "l'apprentissage statistique", en particulier avec les travaux de Vladimir Vapnik. L'idée étant ici de tirer des règles, des "patterns", automatiquement à partir des données. Cette approche restera majoritairement théorique jusqu'au début des années 90 où elle deviendra la technique de référence dans la majorité des problématiques de data science.
Nous pouvons tenter de résumer les 3 principales approches décrites ci-dessus :
Malgré les succès expérimentaux et le puissant corpus théorique qui s’est développé autour des sciences statistiques, les méthodes quantitatives sont restées très contraintes jusqu’au milieu du 20ème siècle, pour la raison suivante : les données étaient rares, coûteuses à acquérir et à traiter. A titre d’exemple, le recensement américain de 1880 a nécessité plus de sept années, pour collecter et analyser les données (Source Wikipedia) ! Contrairement à aujourd’hui, les données n’étaient pas massivement générées par des capteurs ou des formulaires en ligne. Elles devaient être récoltées manuellement avec beaucoup de patience. Qui plus est, même si beaucoup de données auraient pu être accumulées, elles n’auraient ensuite pas pu être traitées. Pas de calculatrices, et encore moins d’ordinateurs : les calculs étaient fastidieusement réalisés à la main, par des human computers (Grier 2006).
Il faut donc bien garder à l’esprit que toutes les méthodes phares, encore aujourd’hui enseignées en statistiques, ont été inventées dans ce contexte particulier de_(very) small data_ et de capacités computationelles limitées. Une des méthodes les plus utilisées en statistiques exploratoires, l’analyse en composantes principales, a été proposée par Karl Pearson en 1901, dans un article illustrant l’algorithme par une application à dix observations dans un espace à deux dimensions (Pearson 1901). Autre exemple : en réutilisant sa méthode des moindres carrés, Gauss a modélisé en 1810 l’orbite de l’astéroïde Pallas sur la base de 6 observations (Chabert 1989). De façon générale, en inférence statistique, on admet que la plupart des méthodes sont valables dès qu’on a affaire à des échantillons d’au moins 30 observations (Dodge 2007). Dans ce contexte, les statistiques inférentielles se construisent sur une hypothèse très forte : les modèles prédictifs se construisent uniquement à partir d’un modèle théorique et les données ne servent qu’à tester l’adéquation des mesures à ce modèle théorique, en les extrapolant à une population mère beaucoup plus vaste que l’on n’est (hélas) pas en mesure d’observer (Lebart 2006).
L’essor de l’informatique a eu un impact majeur sur la pratique de la statistique. A partir des années 1960, on a senti que les ordinateurs allaient changer la donne et que les méthodes et outils développés à l’ère des small data n’étaient plus forcément les plus pertinents. Benzécri, un grand nom de la statistique française, inventeur de l’analyse factorielle des correspondances, a affirmé dès 1965 :
Il est impensable d’utiliser des méthodes conçues avant l’avènement de l’ordinateur, il faut complètement réécrire la statistique (Lebart 2006)
Et en effet, même si la statistique n’a pas été entièrement repensée, elle s’est fortement enrichie de nombreux développements méthodologiques tant pour la statistique exploratoire qu’inférentielle, rendus possibles par la puissance de calcul des ordinateurs et des volumes de données de plus en plus importants (Lebart 2006, Adler 2013) :
Contrairement aux hypothèses générales qui sont les hypothèses d’ordre scientifique qui régissent l’étude d’un phénomène et qui précédent la phase d’observation ou d’expérimentation statistique, les hypothèses techniques interviennent dans la mise en œuvre pragmatique des méthodes statistiques. Elles concernent principalement la spécification des modèles et des distributions statistiques impliquées dans ces modèles. Certaines hypothèses techniques n’ont aucun lien avec les hypothèses générales, mais sont au contraire simplement des exigences des modèles utilisés. L’un des principaux obstacles à l’utilisation d’estimateurs robustes (peu sensibles à la présence d’outliers vis-à-vis des distributions étudiées) était la difficulté des calculs à mettre en œuvre. Les panoplies se sont enrichies de procédures plus robustes dès l’apparition de moyens de calculs plus puissants. Pour des raisons analogues, les techniques non-paramétriques qui s’affranchissent des hypothèses les plus lourdes ont connus un regain d’intérêt.
Peu à peu, dans de nombreux domaines, on observe un rejet de l’inférence statistique probabiliste classique, trop rigide et parfois même fausse dans des contextes de données massives : ainsi fleurissent par exemple les articles scientifiques mettant en cause certaines usages de la p-value, l’un des indicateur emblématique de la statistique inférentielle classique (Lambdin 2012, Lin 2013). En 1973, Benzécri écrira (Benzécri 1973) :
sous le nom de statistique mathématique, des auteurs [...] ont édifié une pompeuse discipline, riche en hypothèses qui ne sont jamais satisfaites dans la pratique
Les développements méthodologiques de la science statistique, rendus possibles par le développement de l’informatique et évoqués plus haut (méthodes robustes et non paramétriques, méthodes algorithmiques, rééchantillonnage), vont progressivement rendre poreuses les frontières entre statistiques exploratoires et statistiques inférentielles. En effet, ils rendent possible la modélisation et la prévision, tout en s’affranchissant des contraintes théoriques de l’inférence classique. C’est les données elles-mêmes qui font émerger le modèle. Benzécri prophétisera ce renversement de paradigme par la phrase suivante (Benzécri 1973) :
le modèle doit suivre les données et non l’inverse
Cette nouvelle façon d’envisager l’analyse de données n’est bien sûr pas une spécificité française. Avec un article fondateur de 1962 dans lequel il exprime ses doutes sur la statistique mathématique classique (Tukey 1962), Tukey a initié le mouvement l’exploratory data analysis (EDA). Ce mouvement aura une influence majeure sur l’analyse de données du 21ème siècle.
La pratique du métier de data scientist prouve effectivement que Tukey et Benzécri avaient vu juste. Dans notre métier, c’est désormais principalement le traitement massif exploratoire de données qui contribue à la production de connaissances. Les méthodes inférentielles classiques se confinent à des champs de plus en plus restreints, telles que les études cliniques par exemple. Et même dans ces domaines très spécialisés et très encadrés, ces approches basées sur une stricte application de la statistique mathématique sont de plus en plus régulièrement critiquées. Par exemple, le chirurgien Laurent Alexandre prône pour un passage de la déduction vers l’induction pour l’analyse des données médicales, et par une création de connaissances plus proche de la réalité, tirées de données massives plutôt que par la création de modèles comportementaux “moyens” (Alexandre 2011).
Concrètement, cela se matérialise par le fait que, grâce aux rééchantillonnage sur de grands volumes de données, les techniques exploratoires et algorithmiques, pourtant éloignées de la statistique mathématique, s’insèrent de plus en plus dans les techniques d’inférence. L’extraction de régularités dans les données devient un moyen de prédiction, du moment que l’on est capable de les valider grâce aux techniques de rééchantillonnage. Comme le montre Lebart, l’exploration n’est plus une simple contemplation des données, l’inférence et la prédiction deviennent même une exigence de l’utilisation actuelle des démarches exploratoires (Lebart 2006). C’est d’ailleurs pour cela qu’il a complètement remanié la 4ème édition de son livre Statistique exploratoire multidimensionnelle, un classique de l’analyse exploratoire, pour mettre l’inférence au coeur de chacune des méthodes exploratoires présentées.
C’est sur cette base qu’est majoritairement pratiquée la data science contemporaine : oubliant la statistique mathématique, elle s’appuie quasi exclusivement sur la combinaison de méthodes d’analyse de données assez anciennes avec une pratique systématique du rééchantillonnage.
La data science telle qu’elle est couramment pratiquée aujourd’hui se base effectivement sur l’utilisation d’algorithmes assez simples et anciens, boostés au rééchantillonnage, utilisés très empiriquement, sans recours au cadre formel de la statistique mathématique. Illustrons cela par deux pratiques très courantes dans les solutions gagnantes des concours en ligne de data science (comme Kaggle, pour ne citer que lui (Site Kaggle)) :
La pratique du métier de data scientist est aujourd'hui assez éloignée des objectifs initiaux de l'intelligence artificielle, i.e. reproduire des capacités de raisonnement humain. Notre métier est dirigé par les données et par des KPI métier à optimiser mais l'homme reste au coeur du processus d'interprétation et d'utilisation de ces modèles. Nous sommes néanmoins à une étape clé car les techniques d'apprentissage statistique et les technologies big data nous permettent aujourd'hui :
Nous arrivons donc aujourd'hui à extraire des règles automatiquement et sans expert humain, mais ces règles sont des "objets" statistiques qui ne sont pas encore manipulés automatiquement par la machine. De la même façon, la majorité des algorithmes de machine learning doivent être supervisés, i.e. nous devons leur fournir une cible à modéliser. Nous sommes encore loin d'algorithmes intelligents qui pourraient extraire automatiquement à la fois des patterns dans les données et une cible permettant de résoudre le problème métier.
Il est intéressant de remarquer que les modèles de la data science contemporaine ne sont pas sans conséquences sur la production de connaissances. En effet, on constate que plus les modèles sont performants en terme précision et de capacité prédictive, plus ils sont difficiles à interpréter, pour les raisons suivantes :
Ce compromis entre performance des modèles et interprétation humaine est bien connu (Kuhn 2013). Certains chercheurs et praticiens tentent de mettre en place des méthodes visant à favoriser l’interprétation des modèles complexes, mais l’usage de ces méthodes reste limité et, comme l’indique Kuhn, est-il vraiment nécessaire de chercher à interpréter un modèle efficace ? (Kuhn 2013)
As long as complex models are properly validated, it may be improper to use a model that is built for interpretation rather than predictive performance.
Ainsi, nous construisons actuellement des modèles ultra-performants, mais que nous ne comprenons plus toujours... une manière d’interpréter ce phénomène est que la data science actuelle tend à produire des concepts qui dépassent la capacité d’abstraction humaine. L’homme serait peu à peu mis à l’écart des productions de connaissances : les modèles qu’il a mis en place seraient capable de prédire beaucoup de phénomènes, dans énormément de champs de connaissances (les méthodes de data science sont génériques), sans lui révéler leurs secrets, c’est-à-dire les interactions fines entre variables qui font que le modèle marche si bien. Et ceci n’est qu’un premier pas : comme nous l'avons vu, la data science telle que nous l’avons présentée jusqu’ici est une forme élémentaire et fruste d’apprentissage machine, un simple premier pas vers l'apprentissage et l'intelligence artificielle de demain.
Nous l'avons déjà évoqué : depuis les années 1960, la science développe peu à peu une théorie de l’apprentissage des machines, qui a pour objectif d’aller au-delà de la mécanisation de schémas répétitifs et déterministes. Vapnik est l’un des fondateurs de cette discipline, qui pose les fondements de l’intelligence artificielle basée sur l’apprentissage à partir des données. Il a ainsi défini la dimension VC (pour Vapnik-Chervonenkis) qui est une mesure de la capacité d'un algorithme à apprendre et à généraliser. Dans ces développements, l'intelligence est pour le moment réduite à apprendre automatiquement des règles à partir des données.
Ces algorithmes sont majoritairement supervisés, i.e. ils ont besoin d'un objectif mesurable, d'un professeur pour pouvoir extraire des règles et ils nécessitent de nombreux (très nombreux) exemples. Ce point est crucial car il marque la différence principale entre l'apprentissage humain et l'apprentissage machine. L'Homme a la capacité d'apprendre à la fois de manière non-supervisée (sans professeur en se reposant uniquement sur ses expériences) et avec une grande économie de données (nous n'avons pas besoin de répéter une expérience plusieurs milliers de fois pour l'assimiler).
Cependant, d'autres classes d'algorithmes montrent des résultats impressionnants avec notamment le deep learning. Nous sortons ici complètement du cadre des outils d’analyses évoqués jusqu’à présent. Ces algorithmes permettent aux machines de s’alimenter automatiquement en concepts dépassant largement la capacité d’abstraction humaine, comme par exemple le dernier né de Google Deepmind, AlphaGo. Cet algorithme combine à la fois de l'apprentissage supervisé (pour apprendre des règles à partir de parties jouées par des experts), et de l'apprentissage par renforcement (en jouant contre lui-même des millions de parties). Il y aurait beaucoup à dire au sujet du deep learning, nous y reviendrons dans un futur article de blog !
Cette capacité de combiner différents mode d'apprentissage en permettant à la fois d'apprendre des experts et de leurs propres expériences se rapprochent de plus en plus des capacités humaines. Une étape à franchir pour égaler l'humain dans de nombreux problèmes est la capacité à généraliser avec peu de données et à utiliser des expériences dans d'autres domaines pour intuiter de nouveaux résultats.
Dans notre métier de data scientist, une tendance généralement observée est que la place de l’Homme dans le mécanisme de formalisation du monde est successivement passée d’artisan à spectateur. Nous nous reposons sur des algorithmes capables d'extraire et de manipuler des concepts qui nous deviennent inaccessibles. Cette place laissée aux algorithmes ne cesse de grandir au nom de l'efficacité de nos sociétés. Après les révolutions des secteurs primaires, puis secondaires, nous allons observer dans les prochaines années une révolution du secteur tertiaire ou de nombreux métiers seront automatisés. Des données de plus en plus nombreuses et variées ne feront qu'accentuer ce phénomène : la machine qui reproduit désormais des fonctions humaines (vision, etc.), mais devient aussi capable de capter des signaux physiques, chimiques, sociaux, etc. inaccessibles à l’humain moyen (accéléromètre, oxymètre, activité sur les réseaux sociaux...). Le monde devient de plus en plus mesurable, multidimensionnel et analysable par la machine. Quelles seront les limites de la production de connaissances ?
. Les lois de la pensée, p. 21. (1992).
Russell Ackoff. From data to wisdom. Journal of Applied Systems Analysis 16, 3–9 (1989).
Yuri P. Adler. The statistics: past, present, and future. (2013).
Laurent Alexandre. La mort de la mort. (2011).
José M. Arribas. Les débuts de la statistique mathématique en Espagne. Mathematics and Social Sciences 166, 25–45 (2004).
Jean-Paul Benzécri. L’Analyse des Données, t.1 : Taxinomie ; t.II : L’Analyse des Correspondances. (1973).
George Boole. An investigation of the laws of thought on which are founded the mathematical theories of logic and probabilities / by George Boole.. (1854). Link
Leo Breiman, Jerome Friedman, Charles J. Stone, R.A. Olshen. Classification and regression trees. (1984).
Léo Breiman. Random forests. Machine Learning 45, 5–32 (2001).
Jean Luc Chabert. Gauss et la méthode des moindres carrés. Revue d’histoire des sciences 42, 5–26 (1989).
Alain Desrosières. La politique des grands nombres. (2010).
Yadolah Dodge. Statistique - Dictionnaire encyclopédique. (2007).
Jean-Jacques Droesbeke, Philippe Tassi. Histoire de la statistique. (1990).
J. Gasser. A Boole Anthology: Recent and Classical Studies in the Logic of George Boole. (2000). Link
David Alan Grier. When computers were human. (2006).
Max Kuhn, Kjell Johnson. Applied predictive modeling. (2013).
Charles Lambdin. Significance tests as sorcery: science is empirical - significance tests are not. Theory and Psychology 22, 67–90 (2012).
Ludovic Lebart, Marie Piron, Alain Morineau. Statistiques exploratoire multidimensionnelle. (2006).
Gottfried Leibniz. Dissertatio de arte combinatoria. (1666). Link
G. W. Leibniz.
G. W. Leibniz. Nova methodus pro maximis et minimis. Acta Eruditorum (1684).
Mingfeng Lin, Galit Shmueli Henry C. Lucas. Too big to fail: large samples and the p-value problem. Information Systems Research 24, 906–917 (2013).
G. Martin, M. Régnier. Leibniz: logique et métaphysique. (1966). Link
Karl Pearson. La grammaire de la science. (1912).
Karl Pearson. On lines and planes of closest fit to systems of points in space. Philosophical Magazine 2, 559–573 (1901).
Michel Serfati. A la recherche des Lois de la Pensée. Sur l’épistémologie du calcul logique et du calcul des probabilités chez Boole. Link
John W. Tukey. The future of data analysis. The Annals of Mathematical Statistics 33, 1–67 (1962).
G.W.F. von Leibniz, L.E. Loemker. Philosophical Papers and Letters: A Selection Translated and Edited, with an Introd. (1969). Link
M. E. Boole 1905, quoted in Laita 1976, 243
A Symbolic Analysis of Relay and Switching Circuits, C. Shannon Master thesis (1937)
Logical vs.Analogical or Symbolic vs. Connectionist or Neat vs. Scruffy, Marvin Minsky.