Cet article est le premier d’une série de communications, visant à partager les pratiques usuelles en statistiques et analyse de données au sein de la communauté OCTO. Chez OCTO, notre vocation est de faire de l’IT et des Big Data, mais il est important de savoir que beaucoup de concepts utilisés dans les algorithmes analytics avancés s’appuient sur des fondements statistiques classiques. Connaître ces fondements permet de mieux comprendre les implications (théories sous-jacentes, limites, etc.) des solutions analytics/Big Data. Par ailleurs, l’application directe de certaines méthodes statistiques permet de répondre aux besoins de certains de nos clients, alors pourquoi nous en priver ? Et oui, parfois nous avons affaire à des volumes de données limités, à des données bien structurées dans des fichiers propres… et dans ce cas, la statistique peut nous aider, alors profitons-en !
Dans cet article, nous proposons une introduction à la comparaison statistique de populations. L’objectif général est de tester si deux ou plusieurs échantillons proviennent d'une même population mère, pour une ou plusieurs variable(s) observée(s). Des ouvrages entiers sont dédiés à ce sujet. En conséquence, cet article ne vise pas à l'exhaustivité. Le but est plutôt de faire prendre conscience au lecteur des enjeux de la problématique de comparaison de populations et des réflexes à acquérir pour mener correctement ce type d'étude.
Pour cela, cet article s'articule de la façon suivante : tout d'abord, nous rappelons brièvement pourquoi la comparaison de populations reste un sujet pertinent dans un contexte Big Data. Ensuite, nous introduisons les grands principes de la comparaison de populations, basée sur la théorie des tests statistiques : cette théorie consiste à définir une hypothèse qui sera validée ou infirmée par le calcul d'une statistique de test. Nous montrons alors comment ces tests peuvent être mis en oeuvre dans un cadre paramétrique. Dans un premier temps, il faut être capable de bien comprendre le contexte du test (cas d'application et contraintes de mise en oeuvre), qui va nous amener à la sélection d'une statistique de test adaptée. L'enjeu pour le praticien se situe essentiellement à cette étape. A titre d'exemple, nous fournissons un aperçu de la diversité de statistiques de tests pouvant exister dans divers cas d'application. Cependant, une fois la statistique choisie, le calcul de la statistique et l'acceptation ou le rejet de l'hypothèse du test se fait aisément grâce aux suites logicielles disponibles, comme nous le montrons dans la dernière partie de cette article.
Le principe la comparaison de populations est de tirer des conclusions sur une population à partir d’échantillons. Les fondements théoriques modernes de la théorie des tests, utilisée à cet effet, ont été posés entre 1926 et 1933 par Jerzy Neyman et Egon Pearson. Selon certains auteurs, cette problématique peut sembler obsolète dans un contexte Big Data : si les Big Data permettaient d'observer une population dans son ensemble (N = all), il n'y aurait plus grand intérêt à travailler sur des échantillons (voir par exemple http://www.foreignaffairs.com/articles/139104/kenneth-neil-cukier-and-viktor-mayer-schoenberger/the-rise-of-big-data).
Néanmoins, N = all n’est pas encore la norme dans les analyses. Diverses contraintes méthodologiques et technologiques peuvent conduire à la nécessité de travailler sur des échantillons : puissance de calcul limitée, temps de traitement, complexité des manipulations de données, etc. De plus, le N = all disponible dans les bases de données analysées par nos algorithmes est-il vraiment le reflet de l’ensemble de la population ? N’existe-t-il pas des comportements non-mesurés, incitant à modérer toute conclusion ? A cette question épistémologico-mathématique, j’espère apporter des pistes de réflexion dans un prochain article. Quoiqu’il en soit, si N < all, les statistiques peuvent nous aider !
Une comparaison de populations se base sur un test. On pose une hypothèse nulle (H0) d’équivalence de deux ou plusieurs échantillons, pour une ou plusieurs variables d’intérêt mesurée(s). Une hypothèse alternative est également formulée (H1). De ces choix dépendront la nature du test : on parle de test bilatéral si H1 suppose que les deux échantillons ne sont pas équivalents et de test unilatéral si H1 formule une hypothèse de supériorité ou d'infériorité entre les deux échantillons. Cette distinction ne sera pas développée dans cet article, qui se placera dans le cadre de tests bilatéraux. On choisit alors un test statistique qui permettra d’accepter ou de rejeter l'hypothèse nulle. Puisque l’on ne considère pas l’ensemble des individus étudiés (N < all), ce test se fait dans un cadre probabiliste. Pour choisir ce test, deux points doivent être éclaircis :
Par soucis de concision, nous restreindrons cet article aux tests paramétriques, qui posent une hypothèse a priori de distributions des variables considérées.
Comme nous le verrons, les tests ne sont généralement pas compliqués à réaliser : la plupart du temps, ils sont directement disponibles dans les distributions logicielles statistiques. La difficulté réside plutôt dans la sélection du test adapté à la situation. Pour faire ce choix, il faut pouvoir répondre à un certain nombre de questions :
Le cas d'application étant clarifié, il faut également questionner les conditions de mise en oeuvre de la statistique de test. En effet, la sensibilité d'un test à un certain nombre de facteurs peut biaiser ses résultats. Tout d'abord, dans un cadre paramétrique, l'hypothèse concernant la distribution des variables considérées doit être vérifiée : dans le cas de variables continues, elles sont généralement considérées comme normales ou multinormales (dans le cas de variables discrètes, cette hypothèse est moins importante, pour des raisons théoriques que nous ne développerons pas ici). Par ailleurs, d'autres facteurs peuvent biaiser la conclusion d'un test : présence de points atypiques, taille de l'échantillon...
Concernant l'hypothèse de normalité, précisons qu'elle admet une certaine souplesse : on peut transformer les variables pour se rapprocher du cadre gaussien, le théorème central limite établit que l’on tend vers une loi normale lorsque les effectifs augmentent, et certaines statistiques de test sont intrinsèquement peu influencées par un écart à cette hypothèse. De façon générale, la statistique robuste est un domaine d'étude riche, qui vise à limiter les divers biais que peuvent induire les contraintes de mise en oeuvre des méthodes statistiques. Ainsi, on trouve souvent dans la littérature des versions robustes de tests statistiques pour les différents cas d'application.
Au final, la considération du cas d'application et des contraintes de mise en oeuvre va amener à choisir le test statistique idoine. Chaque test se base sur une statistique et des principes théoriques spécifiques, que nous ne détaillerons pas dans le cadre de cet article. Toutefois, afin de donner une idée de la diversité de ces situations, le paragraphe suivant indique quelques tests adaptés à différents cas d'application.
Sans viser l'exhaustivité, l'objectif de ce paragraphe est de donner un premier tour d'horizon des différents types de tests qui pourraient être utiles au lecteur. Comme nous le verrons plus loin, il n'est pas forcément nécessaire de savoir calculer les statistiques de chacun de ces tests manuellement pour réaliser correctement une comparaison de population : la plupart des calculs peuvent être réalisés via des logiciels de statistiques. A titre d'illustration, nous indiquons comment réaliser les différents tests suggérés avec le logiciel R (les accolades indiquent la librairie où l'on peut trouver la fonction mentionnée : remarquons que la majorité des tests est directement disponible dans l'installation de base de R). Attention cependant : même si la réalisation du test n'impose pas de maîtriser de toutes les étapes de calcul de la statistique, un minimum de connaissance théorique reste nécessaire pour un usage avisé du test et de la fonction.
| Type de comparaison | Nombre d'échantillons | Test | Dans R |
| Comparaison de moyenne | 2 moyennes | 1. Test de Student si variances égales 2. Test d’Aspin-Welch si variances inégales | 1. {base} t.test avec var.equal = TRUE 2. {base} t.test avec var.equal = FALSE |
| ≥ 2 moyennes | ANOVA à un facteur (principe de décomposition de la variance) | {base} aov | |
| Comparaison de variance | 2 variances | Test de Fisher | {base} var.test |
| > 2 variances | 1. Test de Bartlett 2. Robustes : test de Levene et tests de Brown-Forsythe | 1. {base} bartlett.test 2. {car} leveneTest avec paramètre center = mean, mean + trim ou median |
| Type de comparaison | Nombre d'échantillons | Test | Dans R |
| Comparaison de moyenne | 2 moyennes | Idem échantillons indépendants, appliqué à une variable aléatoire D dont les valeurs sont obtenues par différences des paires de valeurs, dont on suppose que la moyenne est égale à 0 | {base} t.test avec paramètre mu = 0 |
| ≥ 2 moyennes | ANOVA à deux facteurs (facteur 1 : les échantillons ; facteur 2 : les individus liés). Attention à la mise en œuvre : on rentre progressivement dans le domaine complexe des plans d’expériences. | {base} aov | |
| Comparaison de variance | 2 variances | Test de Pitman | {PairedData} 1. Appariement des vecteurs avec paired 2. Test avec var.test |
| Type de comparaison | Nombre d'échantillons | Test | Dans R |
| Comparaison de moyenne | 2 moyennes | T² de Hotelling (calcul de la variable aléatoire D si les échantillons sont appariés) | {ICSNP} HotellingsT2 |
| ≥ 2 moyennes | MANOVA avec différentes statistiques de test : Wilks ou transformations robustes (Pillai, Hotelling, Roy) | {base} manova puis summary avec la statistique désirée | |
| Comparaison de variance | ≥ 2 variances | Généralisation du test de Bartlett | {base} bartlett.test |
| Type de comparaison | Test | Dans R |
| 2 proportions | 1. Si la taille des échantillons > 30 individus et que le nombre d’individus avec le caractère Z dans chaque échantillon est > 5 : statistique U 2. Si quel que soit le nombre d’individus, le caractère Z dans un des échantillons est < 5 : test exact de Fisher 3. Si la taille de l’un des échantillons est < 30 et que le caractère Z est > 5 dans les échantillons : test d’homogénéité du χ² | 1. Calcul manuel 2. {base} fisher.test 3. {base} chisq.test avec paramètre correct = FALSE |
| > 2 proportions | 1. Si le caractère Z dans un des échantillons est < 5 : test exact de Fisher 2. Si le caractère Z dans un des échantillons est > 5 : test du χ² | 1. {base} fisher.test 2. {base} chisq.test avec paramètre correct = FALSE |
Les noms des tests peuvent sembler barbares, leurs fondements théoriques abscons… mais rassurez-vous, leur mise en œuvre est aisée. Quasiment tous existent déjà dans les distributions logicielles existantes (mais attention, le prérequis indispensable est de savoir identifier le test adapté au contexte).
Le petit exemple ci-dessous permet de démystifier le test statistique et de montrer avec quelle facilité on peut le réaliser avec le logiciel R.
Considérons l'exemple bien connu suivant : sur quatre îles sont réalisées des poteries et on aimerait savoir si les compositions en aluminium, fer, magnésium, calcium et sodium des poteries sont les mêmes quelle que soit l’île. Pour cela, on prélève 26 poteries sur les différentes îles. On a donc un tableau de 26 individus avec 6 variables (5 variables continues : teneurs en aluminium, fer, etc. et une variable catégorielle : île d’origine). La question à laquelle nous cherchons à répondre est alors : les teneurs en aluminium, fer, etc. sont-elles les mêmes quelle que soit l’île d’origine ? Autrement dit, si µ1, …, µ4 représentent les barycentres des teneurs en aluminium, fer, etc. des quatre îles d’origine, on cherche à tester H0 : µ1 = …= µ4. Si H0 est rejetée, c’est qu’au moins deux des vecteurs moyennes sont différents et que les poteries des diverses origines ne sont pas toutes équivalentes.
Une telle comparaison de plusieurs échantillons dans un espace multidimensionnel correspond à une MANOVA (généralisation multidimensionnelle de l’ANOVA). Les principes de la MANOVA sont explicités ici : https://onlinecourses.science.psu.edu/stat505/node/162. Ne nous laissons pas impressionner par les formules, H0 va être testée en un petit coup de R :
pot <- read.csv2("poterie.csv")
On a bien des variables continues (Aluminium, Iron…), selon des origines (Site) :
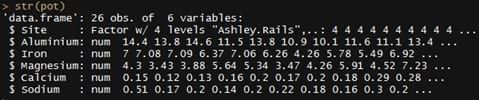
## Table des Variables d'intérêts
X <- cbind(pot$Aluminium, pot$Iron, pot$Magnesium, pot$Calcium, pot$Sodium)
## Populations à comparer
Y <- pot$Site
## MANOVA
model <- manova(X ~ Y)
summary(model, test = "Wilks")
et on obtient :

Nous avons utilisé la statistique de Wilks, cas de base de la MANOVA. Elle correspond au ratio entre la variabilité intra-classe et la variabilité totale des échantillons. Si elle tend vers 0, c’est que pour chaque sous-population, les points sont agglutinés autour de leurs barycentres et on aura tendance à rejeter H0 (c’est bien le cas : on voit qu’elle est égale à 0.012301).
Généralement, la statistique de Wilks est peu utilisée car sa distribution est difficile à appréhender. La plupart du temps, on a recours à des transformations, qui permettent de la rapprocher d'une loi plus connue (par exemple, la transformation de Bartlett permet de se rapprocher d’une loi du χ² ou la transformation de Rao d’une loi de Fisher). Citons également d'autres transformations connues car plus robustes : trace de Pillai, trace de Hotelling-Lawley… On peut les utiliser simplement en changeant le paramètre ‘test’ ("Wilks", "Pillai", "Hotelling") dans la commande ‘summary’.
L’interprétation des valeurs de ces statistiques peut être difficile si l’on ne connaît pas les théories sous-jacentes : il faut savoir analyser la région critique et le niveau de signification, selon la nature du test, de la loi de probabilité de la statistique de test. Mais pas de panique : heureusement, une valeur va nous permettre de conclure sans équivoque au rejet ou non de H0, quel que soit la statistique utilisée. C’est la p-value du test. En effet, si p-value ≤ risque d’erreur du test (=5% par défaut), on rejette H0 (voir http://freakonometrics.hypotheses.org/2462 pour une discussion intéressante sur ce concept). En l’occurrence ici, on voit que la p-value est quasi nulle (Pr(>F) = 1.84e-12), donc H0 peut être rejetée pour un risque d’erreur de 5% : au moins deux des vecteurs moyennes sont différents, les poteries ne peuvent pas être considérées comme équivalentes quelle que soit leur origine.
La théorie de la comparaison de populations est un vaste domaine de la statistique, que nous n’aurons fait qu’effleurer ici : certains concepts ont été à peine cités (nature, robustesse) , d'autres éléments importants n'ont pas été développés, pour éviter de complexifier cet article introductif (risque d'erreur de première et dernière espèce, puissance d'un test ). Néanmoins, j’espère que cet article aura apporté au lecteur une première introduction à la comparaison de populations et aura mis en avant certaines idées :