Nous allons voir dans cet article comment un calcul complexe peut être exécuté plus rapidement sur plusieurs machines. Notre calcul consistera à valoriser, c'est à dire à déterminer le prix d'un portefeuille de produits financiers détenus par une banque d'investissements. Il existe en effet pour ces calculs de pricing des algorithmes adaptés à une architecture en grille de calcul, car ils peuvent être décomposer en un ensemble de calculs unitaires. Ces calculs de pricing consistent à effectuer des simulations d'évolution de prix se basant sur son historique et sur des modèles mathématiques. Ils sont utilisés quotidiennement de nos jours dans les salles de marché. Tout d'abord, nous allons définir ce qu'est une grille de calcul et expliquer son intérêt. Puis nous présenterons un exemple d'algorithme de pricing : le calcul du prix d'une option. Nous présenterons ce qu'est une option et les grandes lignes de ce calcul. Suivra une partie un peu technique, faisant appel à quelques notions sur les lois statistiques pour entrer plus en détail dans cet algorithme. Cette partie peut être ignorée en première lecture sans perte d'information. Nous expliquerons ensuite comment cet algorithme sera exécuté sur une grille à travers les extraits de code d'une application exemple. Enfin nous conclurons par quelques mesures sur les gains de performances apportés par une grille de calcul.
Une grille est une architecture informatique dans laquelle un ensemble de ressources distribuées sont coordonnées entre elles autour d'un objectif commun. Ces ressources sont des ordinateurs dont on souhaite utiliser les processeurs pour réaliser un calcul complexe. Ils peuvent être distribués, c'est-à-dire distants physiquement, à condition d'être reliés par un réseau informatique. Je prendrai la convention de réserver le terme cluster pour la gestion de la haute disponibilité (High Availability cluster) et grille pour la gestion de la performance, même si la dénomination peut varier selon les interlocuteurs. Comme nous l'avons vu dans un précédent article, l'architecture en grille est aujourd'hui en train de supplanter l'utilisation de grands systèmes. En effet, l'utilisation de plusieurs machines d'entrée de gamme se révèlent, pour les calculs que nous détaillerons, moins chère qu'un grand serveur et permet plus facilement d'augmenter la puissance en ajoutant des machines.
Sur les bourses s'échangent des actions mais aussi des contrats nommés options d'achat qui donnent le droit, mais pas l'obligation, d'acquérir une action à une date future et à un prix donné. Prenons un exemple : j'achète aujourd'hui pour 5 ? le droit d'acheter dans 1 an l'action A à un prix noté K : 15?. Dans un an, l'action A vaudra un prix S, par exemple 21?. Et le contrat d'option vaudra Max(S-K,0) = 21-15=6? car il permettra de recevoir l'action pour K=15? et de la revendre immédiatement pour S=21? et d'empocher la plus-value de 1?. Dans le cas où S
Tout l'objectif consiste à estimer le prix de cette option au jour d'aujourd'hui. Est-ce que 5? est un bon prix?
Pour cela, on utilise un modèle mathématique appelé arbre binomial de Cox-Rubinstein. Dans ce modèle simplificateur, le temps et le prix de l'action sous-jacente (ici l'action A) évoluent de manière discrète. A chaque étape le cours de l'action peut augmenter d'un facteur Up ou diminuer d'un facteur Down selon une probabilité p.
Les scénarios possibles d'évolution du prix se représentent sous forme d'un arbre.
Pour les plus pressés, l'estimation du prix revient à parcourir l'arbre récursivement. Ces algorithmes étant statistiques, les cas réels portent sur des arbres à plusieurs centaines voire plusieurs milliers de niveaux. De tels algorithmes, très gourmands en calcul, sont donc de bons candidats pour être portés sur une grille de calcul. Les personnes pressées ou ne souhaitant pas explorer le modèle mathématique pourront passer directement au paragraphe concernant l'implémentation de l'algorithme sur une grille sans perte d'information.
Mais pour l'instant, précisons la construction de cet arbre : Je noterai par la suite : S ou de manière équivalente S(t) : le prix actuel du sous-jacent : c'est à dire l'option A C ou de manière équivalente C(t) : le prix actuel de l'option d'achat t : l'instant d'achat de l'option K : le prix d'exercice de l'option : c'est à dire le prix auquel l'option me donne le droit d'acheter l'action à l'échéance T: l'intervalle de temps représenté par un pas n : le nombre de pas tel que t+nT représente l'échéance de l'option, c'est-à-dire la date à laquelle ce contrat me donne le droit d'acheter l'action A au prix convenu (K)
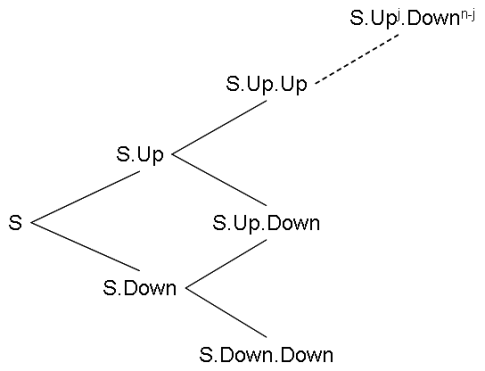
Il faut ensuite déterminer les valeurs pour les pas Up et Down et la probabilité p. Pour cela, l'historique des prix de l'action A est comparé aux modèles mathématiques d'évolution établis par les modèles micro-économiques. Par exemple, la statistique de l'évolution du prix est représentée dans ces modèles par une loi statistique log-normale. On en identifiera la moyenne et l'écart type à partir des données historiques. Dans le modèle simplificateur de l'arbre binomial, à condition d'utiliser un grand nombre de points, les valeurs de l'arbre sont également réparties selon une loi log-normale. La probabilité p de monter du prix et la valeur Up du pas de monter de cet arbre seront fixés de façon à ce que la moyenne et l'écart type de l'ensemble des prix de l'arbre soient identiques à la moyenne et à l'écart type de l'historique des prix de l'action A. L'arbre simulera ainsi les possibilités d'évolution du prix de l'action sous-jacente.
Rappelons que l'objectif d'un arbre est de déterminer le prix de l'option d'achat C.
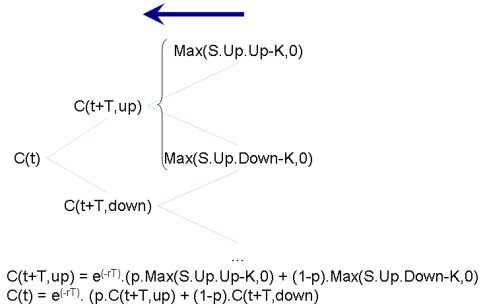
L'arbre est construit jusqu'à la date de l'échéance de l'option : le jour où l'on obtient le droit d'acheter au prix fixé. Les feuilles de l'arbre représentent les valeurs possibles du prix de l'action A à cette date. L'application de la formule Max(S-K, 0) permet de déterminer immédiatement le prix de l'option dans chaque état du marché possible représenté par une feuille de l'arbre.
On utilise ensuite un algorithme de calcul permettant de remonter le temps. Celui-ci se base sur le calcul du prix de l'option à l'instant t-T en fonction des deux valeurs possibles à l'instant t. Cela est possible car les théories mathématiques montrent que
C(t) = e(-rT) (p.C(t+T,up) + (1-p).C(t+T,down) ce qui globalement signifie que le prix à l'instant t est une combinaison des deux prix possibles à l'instant suivant, pondérés par leur probabilité d'apparition - p étant la probabilité d'un prix en hausse, 1-p celle d'un prix en baisse - et diminuée du coup de l'argent sur la période. Nous admettrons que, r désignant le taux d'intérêt sans risque, e(-rT) représente le coût de l'argent sur la période. Le taux d'intérêt sans risque est défini dans cet article en anglais.
En conséquent, en appliquant récursivement cette formule à partir de la droite de l'arbre, nous pouvons déterminer la valeur de l'option à l'instant t initial.
Comme nous l'avons précisé, ces modèles sont statistiques et nécessitent un grand nombre de points pour être précis. Notre exemple comportait deux niveaux mais les modèles réels peuvent en comporter des centaines voire des milliers pour une échéance d'une année. Certaines analyses de risques nécessitent des estimations sur plusieurs années. Enfin le nombre d'options manipulées par une salle de marché est également extrêmement important, chaque option nécessitant son arbre de calcul.
De tels algorithmes sont de bons candidats pour être portés sur une grille de calcul. Nous allons désormais étudier comment utiliser ces outils pour distribuer ces traitements
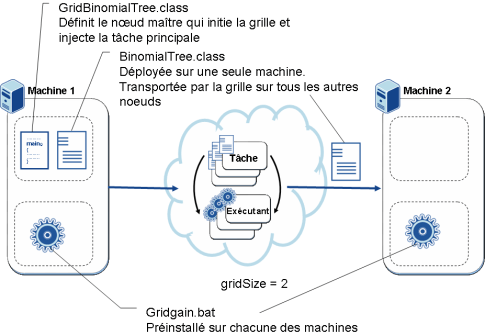
Dans un souci de simplicité et de rapidité, nous avons réalisé cette étude sur un logiciel open source : Gridgain. Ce type de logiciel offre un ensemble de fonctionnalités qui permettent à un code de s'exécuter sur une grille en limitant au maximum le code technique de gestion de la distribution. On peut citer : - la découverte des différents noeuds afin d'établir les échanges réseaux entre eux - le transport du code et des données sur les différents noeuds. Le code est déployé manuellement sur un noeud (celui qui instancie la grille). Il sera automatiquement propagé avec les données sur les autres machines par Gridgain. - l'implémentation du pattern map-reduce que nous étudierons ci-dessous - la gestion de la reprise sur erreur en cas de problème sur un noeud - la répartition de la charge sur les différents noeuds : envoyer le calcul suivant sur la machine la moins chargée - le suivi de la consommation de certaines ressources (processeur...)
Le seul pré-requis est que le logiciel Gridgain soit installé sur chacune des machines.
Gridgain implémente le pattern Map-Reduce. Celui-ci est fondamental pour permettre de distribuer un calcul. Son nom provient des fonctions Map et Reduce des langages fonctionnels comme Lisp. La fonction Map permet d'appliquer une même fonction à tous les éléments d'un tableau. Reduce est une fonction permettant de combiner tous les éléments d'un tableau pour en tirer une valeur unique. Appliquer à la distribution du calcul, ce pattern consiste à rechercher dans la tâche à réaliser un grand nombre de données sur lesquelles on effectuera le même traitement. Dans le cadre du pricing d'un portefeuille d'options, l'hypothèse la plus simple est de considérer chaque option à évaluer comme un ensemble de données sur lequel on appliquera le calcul de l'arbre binomial. La fonction map consistera à effectuer le calcul de prix pour chacune des options du portefeuille. La fonction reduce() sera la somme des valeurs de chaque option afin de connaître la valeur du portefeuille détenu. L'implémentation du pattern Map Reduce
Le code de notre projet est organisé de la manière suivante : - Une classe BinomialTree contient la logique de calcul d'un arbre binomial décrite ci-dessus. Son point d'entrée est l'unique méthode unitTree() dont la signature est la suivante. Elle ne contient aucune dépendance par rapport à la grille et peut être exécutée de manière totalement indépendante. Ce code n'implémente pas le pattern Map/Reduce.
/**
* Construction d?un arbre binomial
* @param stockPrice
* @param strikePrice
* Prix d?exercice
* @param yearsToMaturity
* Période sur laquelle on effectue les calculs
* @param riskFreeRate
* Taux sans risque
* @param volatility
* Variation du titre (risque du titre)
* @param stepNumber
* Nombre de pas pour le calcul de l?arbre
* @param dividend
* Rémunération versée par la société à l?actionnaire
* @return Arbre
*/
public static Double[][] unitTree(
final double stockPrice,
final double strikePrice,
final double yearsToMaturity,
final double riskFreeRate,
final double volatility,
final int stepNumber,
final double dividend)
Une version multi-arbres de cette méthode est définie. Elle permet de définir une liste d'arbres et d'exécuter la méthode unitTree() sur la portion de la liste comprise entre les indices minRange et maxRange. minRange et maxRange permettront ainsi de faire varier le nombre d'options que l'on souhaitera calculer dans le portefeuille et donc le nombre d'arbres différents à calculer.
@Gridify(taskClass = GridifyBinomialTreeTask.class)
public static Double tree(
final List<list> tabList,
int stepNumber,
int minRange,
int maxRange) {
Double[][] tree = null;
for (int i = minRange; i < = maxRange; i++) {
// Récupération des arguments du tableau
final double stockPrice = tabList.get(i).get(0);
final double strikePrice = tabList.get(i).get(1);
final double yearsToMaturity = tabList.get(i).get(2);
final double riskFreeRate = tabList.get(i).get(3);
final double volatility = tabList.get(i).get(4);
final double dividend = tabList.get(i).get(5);
// Appel de la méthode de calcul de l'arbre
tree = unitTree(stockPrice, strikePrice,
yearsToMaturity, riskFreeRate, volatility, stepNumber,
dividend);
}
return tree[0][1];
}
L'exécution de ce code sur une grille en utilisant le pattern Map/Reduce est résumée dans le schéma ci-dessous. Nous allons détailler l'implémentation correspondante.
La classe GridBinomialTreeTask implémente l'ensemble du code technique relatif à la grille. En particulier elle définit une méthode split() qui est ici un synonyme de la méthode Map et une fonction Reduce.
@Override
@SuppressWarnings("unchecked")
protected Collection split(int gridSize, final GridifyArgument arg)
throws GridException{
Object[] args = arg.getMethodParameters();
final List<list>; tabList = (List</list><list>) args[0];
final int stepNumber = (Integer) args[1];
int taskMinRange = (Integer)args[2];
int numbersPerTask = tabList.size()/gridSize;
List jobs = new ArrayList(gridSize);
int jobMinRange = 0;
int jobMaxRange = 0;
for (int i = 0; jobMaxRange < (tabList.size()-1) ; i++) {
jobMinRange = i * numbersPerTask + taskMinRange;
jobMaxRange = (i + 1) * numbersPerTask + taskMinRange - 1;
if (jobMaxRange <= tabList.size()){
jobMaxRange = tabList.size()-1;
}
jobs.add(new GridJobAdapter(jobMinRange, jobMaxRange) {
private static final long serialVersionUID = 1L;
public Double execute() throws GridException {
int min = getArgument(0);
int max = getArgument(1);
// Exécution du calcul de l'arbre
System.out.println("Calcul entre " + min + " et " + max);
return BinomialTree.tree(tabList, stepNumber, min, max);
}
});
}//End for
return jobs;
}
- La méthode split() reçoit en paramètre la taille de la grille et un élément GridArgument contenant le tableau à deux dimensions des paramètres de la méthode tree() vue plus haut. Elle se charge de déterminer le nombre d'arbres que devra calculer chaque noeud de la grille et de créer un GridJobAdapter qui servira de conteneur entre les noeuds.
public Double reduce(List results) throws GridException {
double totalOptionPrice = 0;
//On ajoute les temps retournés par chacun des jobs
for(GridJobResult res : results){
Double optionPrice = res.getData();
totalOptionPrice += optionPrice;
}
//On retourne la valeur du portefeuille
return totalOptionPrice;
}
Les différentes valeurs reçues des différents noeuds sont additionnées afin de fournir la valeur du portefeuille.
- Enfin la classe GridBinomialTree a pour charge d'instancier le noeud maître de la grille : celui qui exécutera les méthodes split() et reduce().
public static void main(String[] args) throws GridException{
if (args.length == 0){
GridFactory.start();
}
else {
GridFactory.start(args[0]);
}
try {
//Création d'un taleau avec les valeurs utiles aux calculs
List tab = new ArrayList(6);
tab.add(stockPrice)
tab.add(strikePrice);
tab.add(yearsToMaturity);
tab.add(riskFreeRate);
tab.add(volatility);
tab.add(dividend);
List tabList = new ArrayList();
//Simulation : création d'un grand nombre de calculs par duplication
for (int i=0; i prix de l'option " + optionPrice);
time = System.currentTimeMillis()-start;
System.out.println("------------------------------");
System.out.println("Execution en " + time + " ms");
System.out.println("------------------------------");
}
finally{
GridFactory.stop(true);
}
}
Lors de l'appel à GridFactory.start(), le middleware GridGain va démarrer une instance de la grille et chercher à découvrir d'autres noeuds. Puis lors de l'appel à BinomialTree.tree(), il va appeler de façon transparente la classe GridBinomialTreeTask grâce à l'utilisation de l'AOP : la programmation orientée aspect. La méthode split() découpera le traitement, produira plusieurs appels à la méthode BinomialTree.tree() avec des données différentes, le middleware enverra ce code et ces données sur les différentes instances qui exécuteront chacune un appel à BinomialTree.tree(). Puis les différents résultats seront rapatriés par le middleware sur le noeud maître qui exécutera la fonction reduce() avant de rendre la main à la méthode main().
En théorie ce genre d'outils permet un passage à l'échelle - ou scalabilité - parfaite. Chaque machine doit pouvoir traiter un nombre d'arbres constant par unité de temps. Tout ajout de machine devrait dès lors se traduire par une réduction du temps de traitement.
Pour le vérifier nous avons calculé la valeur d'un portefeuille de 1500 options en faisant varier le nombre de pas dans l'arbre. Un arbre de 150 pas représente environ 285000 instructions élémentaires de calcul processeur pur, sans aucun appel réseau ni aucune écriture disque. Nous avons d'abord réalisé ce calcul en utilisant uniquement la classe BinomialTree, donc en utilisant un seul thread. Puis nous avons réalisé le calcul sur une grille constituée de deux PC dual-core, donc en utilisant potentiellement 4 threads. Le gain attendu est donc une divison par 4 des temps de traitement. Le graphique suivant représente le rapport entre les temps de traitement sur un ordinateur individuel et sur une grille à quatre noeuds, en fonction du nombre de portefeuilles :
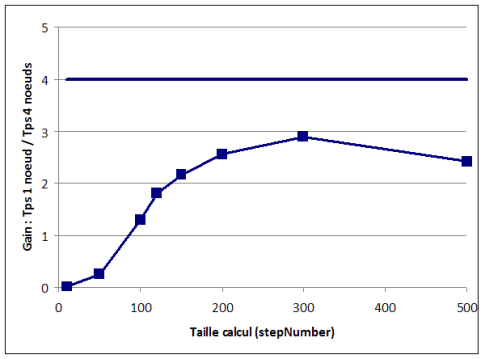
? Le gain maximum mesuré est compris entre 2,5 et 3. ? Le gain n'est pas linéaire. Il dépend du nombre de portefeuilles Ces chiffres montrent que la distribution du calcul sur une grille a un coût. Le middleware doit gérer le découpage, gérer les interactions entre machines ce qui consomme des ressources. De plus les données doivent circuler entre différentes machines ce qui a un coût. Lorsque la taille du calcul augmente, le surcoût lié à la grille est amorti ce qui permet un meilleur ratio. La grille de calcul est donc adaptée à des calculs intensifs. Notons enfin que notre implémentation reste un prototype : au delà de 400 étapes les gains diminuent de nouveau : d'autres optimisations seraient à prévoir. Une autre mesure a ensuite été réalisée en faisant varier le nombre d'options, chacune utilisant un arbre de 150 pas.
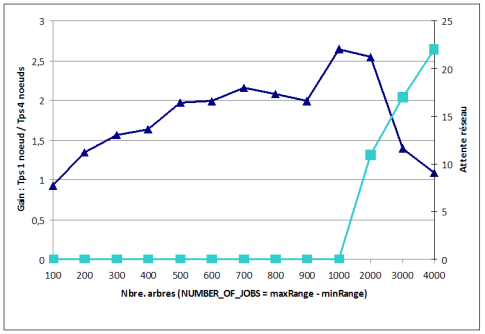
Là encore le gain maximum est inférieur au gain théorique de quatre. Le gain augmente lorsque le nombre de calculs augmente mais au delà de 1000 calculs, le gain chute brutalement. Pour expliquer cela nous devons considérer la courbe bleu claire sur l'échelle de droite. A partir de 1000 calculs la file d'attente réseau se remplit témoignant d'un goulet d'étranglement au niveau du réseau. Les échanges de données imposées par la grille entre les noeuds prennent le pas sur le gain de puissance de calcul. Dans notre cas, cela est dû au fait que notre code exemple présente un défaut : la quantité de données transférées à chaque tâche n'a pas été optimisée. Cependant la conclusion selon laquelle le transfert de données peut devenir un goulet d'étranglement reste valable. Les algorithmes réels sont souvent plus gourmands en données et leurs accès aux données doivent être finement optimisés.
En somme, certains algorithmes particulièrement exigeants en puissance de calcul gagnent à être distribués sur plusieurs machines. Les calculs de pricing, de détermination des prix des instruments financiers en font partie. Les intergiciels de grille de calcul se chargent aujourd'hui d'encapsuler la complexité liée à la distribution et se différencient sur leur capacité de paramétrage et d'optimisation. L'algorithme utilisé sur une grille doit cependant pouvoir respecter le pattern Map/Reduce, ce qui impose d'identifier à l'intérieur de celui-ci un ou plusieurs traitements appliqués à une grande quantité de données. Par rapport à un grand système, une grille de calcul offre une puissance à un coût beaucoup plus faible. Cependant, la scalabilité de ces outils n'est pas immédiate. Les goulets d'étranglements tels que les flux d'informations doivent être soigneusement identifiés. Le découpage des calculs doit être adapté à la grille. Par exemple si chaque calcul est trop petit, la fonction Map devra être modifiée pour regrouper plusieurs calculs entre eux. Au contraire dans le cas d'un arbre trop important son algorithme lui-même devra être découpé. Ce deuxième point est particulièrement complexe car il faut alors identifier à l'intérieur de l'arbre des calculs intervenant sur un ensemble de données. Cela pourrait constituer en soit le sujet d'un autre article.