
En somme, l’apprentissage automatisé désigne l’ensemble des techniques permettant, par voie algorithmique, avec ou sans assistance, de prendre une décision jugée adéquate sur la base d’informations non structurées a priori et inconnues du système auquel elles sont présentées. Cette discipline se caractérise par le fait qu’elle se fonde entièrement sur des méthodes d’induction et de généralisation. La preuve algorithmique n’y est alors plus fondée sur des mécanismes déductifs mais essentiellement probabilistes.
Cet article se propose d’en faire un rapide tour d’horizon et d’exposer le moins formellement possible les notions clefs qui s’y rapportent.
Cet exemple illustre une situation intéressante dans laquelle on présente dans un premier temps au système une liste d’exemples (les parties d’échecs) avec une classification des situations (victoire ou forfait), ainsi qu’un modèle permettant de lier les deux. Dans cette première phase, l’enjeu consiste à raffiner le modèle pour prédire au mieux l’issue d’une partie connue. Dans un deuxième temps, le système est entraîné sur de nouvelles parties (ici contre lui-même). L’enjeu est toujours le même : obtenir le modèle qui indiquera les mouvements à jouer avec les plus grandes chances de victoire possibles. A elle seule, cette première tentative met en œuvre des techniques représentatives des deux grandes familles d’algorithmes d’apprentissage.
Les tâches que cherchent à réaliser des automates entraînés par des techniques d’apprentissage supervisé consistent à effectuer une prévision, de préférence la plus fiable possible, sur la base d’exemples connus. Ce sont des problèmes fréquemment rencontrés dans le cadre de l’analyse prédictive. Voici des exemples typiques de tels problèmes :



En d’autres termes, une question à laquelle une technique d’apprentissage supervisée est susceptible d’apporter une réponse peut se formuler avec des informations connues (« sachant que ») et une variable à évaluer (oui/non, lequel parmi ceux-ci, quelle quantité, etc).
Parmi les exemples cités, on peut distinguer deux catégories de problèmes : les deux premiers répondent à une question ouverte, en l’occurrence la valeur d’une quantité (temps de réponse, nombre de clients), tandis que les deux autres répondent à une question fermée (défaut ou paiement, telle ou telle catégorie d’image). Ces deux types de problèmes répondent respectivement aux noms de problèmes de régression et de problèmes de classification.
Les problèmes de régression cherchent à ajuster un modèle capable d’interpoler une quantité à partir d’un ensemble de variables dont les valeurs sont connues. Le modèle le plus familier est sans doute celui de la régression linéaire, qui calcule une somme pondérée de variables d’entrée (comme le nombre de chambres et la distance à la mer) pour estimer la variable de sortie (comme le nombre de clients sur le mois). Très prosaïquement, le modèle de la régression linéaire donne un résultat du type :
Nombre de clients sur le mois = 0,8 + 21,6*(nombre de chambres) – 2,7*(distance à la mer en km)
Les coefficients en gras sont les paramètres du modèle. Dans le cas de la régression linéaire, il existe une méthode directe pour déterminer leur valeur optimale (celle des moindres carrés). Toutefois, pour des modèles plus complexes, ou lorsque le nombre de variables d’entrée devient trop grand, le calcul direct devient impraticable. On a alors recours à des méthodes algorithmiques d’optimisation pour les déterminer : c’est le domaine d’intervention des algorithmes d’apprentissage.
De manière générale, on va alors chercher à quantifier l’erreur commise par le modèle et à la minimiser. Lorsque l’on aura atteint une marge d’erreur considérée comme acceptable, on considérera que la phase d’apprentissage est terminée et que les valeurs des paramètres du modèle (ici 0,8, 21,6 et -2,7) sont optimales.
Considérons un instant notre exemple en ne prenant en compte que le nombre de chambres de l’hôtel. Supposons que nous disposons d’un historique pour plusieurs hôtels dont nous connaissons le nombre de chambres et la moyenne de fréquentation. Représentons alors cette information sous forme graphique :
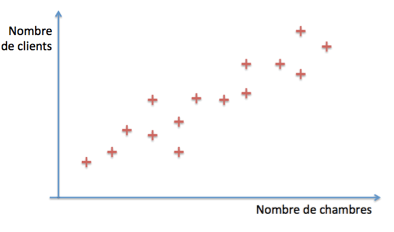
Notre modèle linéaire va chercher à prédire le nombre de clients en fonction du nombre de chambres, sous la forme
Nombre de clients = x0 + x1*(nombre de chambres)
Le but est donc de déterminer x~0 ~ et x1. Une technique simple consiste à commencer par prendre des valeurs arbitraires, par exemple 0 et 1, et à regarder ce que cela donne :
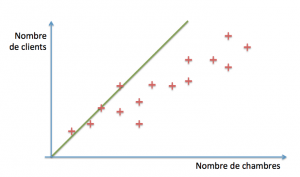
La ligne verte (d’équation clients = 0 + 1*chambres) recoupe les premiers points (disons de une à quatre chambres). Au-delà, en revanche, elle est franchement optimiste. A quel point ? Pour le savoir, nous commençons par évaluer les distances entre le modèle (les valeurs prédites par la droite verte) et nos exemples réels :
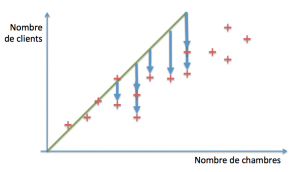
A partir de ces distances, nous construisons une estimation de notre erreur en sommant les carrés des écarts « (nombre réel de clients – nombre de clients prédits)2 ». Cette estimation est appelée « erreur quadratique » et est généralement la mesure adoptée sur les problèmes de régression (le calcul de l’écart peut toutefois changer selon le modèle utilisé).
L’étape suivante consiste à utiliser une technique permettant de réduire cette erreur et d’itérer jusqu’à ce qu’elle reste stable (par exemple ici, en utilisant la descente de gradient qui consiste grosso modo à suivre les flèches bleues). On aura alors atteint une erreur minimale sur l’ensemble des cas connus, et notre modèle sera réputé bien ajusté :
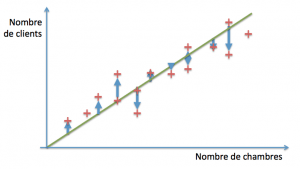
Cette technique est applicable à un nombre arbitrairement grand de variables tant qu’une combinaison linéaire est appropriée. Pour des distributions plus complexes, il existe de nombreuses variantes, comme la régression linéaire localement pondérée, la régression polynomiale avec ou sans régularisation, les fonctions à bases radiales, les arbres de régression… Tous ont en commun la minimisation de l’erreur sur une base d’exemples.
Intéressons-nous maintenant aux problèmes de type « question fermée ». Ils sont qualifiés de problèmes de classification. Le but n’est cette fois plus de prédire une quantité mais de choisir une réponse parmi une liste bien définie.
Autrement dit, la classification a pour but de séparer les individus d’un échantillon en plusieurs catégories bien identifiées, appelées classes. La plupart des algorithmes d’apprentissage destinés à réaliser cette tâche distinguent deux classes seulement, et se généralisent aux problèmes multi-classes par composition de classifications binaires (classe n°1 vs autres classes possibles, classe n°2 vs autres classes, etc).
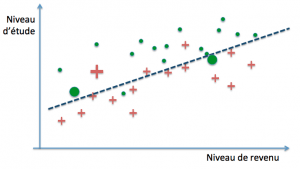
Le modèle à déterminer aura donc la propriété inverse d’un modèle de régression : au lieu de chercher à approcher au mieux les exemples, il va tenter de les séparer au mieux, en commettant le moins d’erreurs possibles. Considérons le cas où nous disposons, en tant qu’organisme de crédit, du niveau de revenu et du niveau d’étude de clients à un contrat de crédit, ainsi que, parmi eux, de la liste de ceux qui ont eu un incident de paiement. L’objectif de l’apprentissage consiste à paramétrer un modèle capable de prédire, à partir des revenus et du niveau d’étude d’un nouveau client, s’il risque de faire défaut au cours de la durée du contrat. Nous allons représenter notre base d’exemples sous la forme d’un nuage de points répartis sur les axes (études, revenus) en faisant figurer par des croix rouges les incidents de paiement, et par des points verts les remboursements sans incidents :
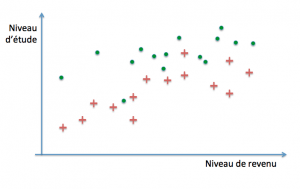
Notre modèle va chercher à tracer une frontière entre les deux catégories qui délimitent de la manière la plus fiable possible les régions dans lesquelles nous pourrons raisonnablement parier trouver de nouveaux clients qui feront défaut pendant la durée du remboursement, d’une part, et d’autre part où se trouveront ceux qui ne connaîtront pas d’incident.
Pour mesurer notre erreur, la mesure la plus immédiate, qui est celle généralement adoptée dans les problèmes de classification binaire, est la proportion d’exemples mal classés : ce sont ceux que nous allons chercher à éliminer.
La question qui se pose alors, compte tenu du fait que nous ne disposons que d’exemples et que le but ultime est de parvenir à des prédictions correctes sur de nouveaux cas, est de savoir quand un modèle parviendra à un bon niveau de généralisation. Dans notre exemple, il est parfaitement possible de définir des frontières de décision arbitrairement précises :
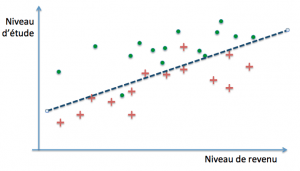
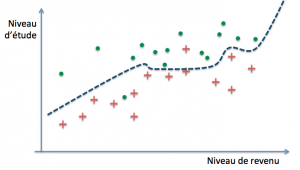
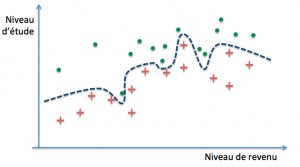
Ces trois modèles pourraient par exemple définir leur frontière de décision par des polynômes de degré croissant. Le premier modèle classe mal trois exemples parmi trente (deux rouges et un vert), le second deux (un rouge et un vert), tandis que le dernier ne commet aucune erreur… sur notre base d’exemples. On dit dans ce cas que les deux premiers ont un biais plus grand que le troisième (ils se trompent davantage). La performance obtenue s’est fait au moyen de la minimisation de l’erreur d’entraînement, encore appelée erreur d’apprentissage.
Qu’en est-il de leur capacité respective de généralisation ?
Erreur d’entraînement et erreur de généralisation Imaginons que l’on introduise dans notre base d’exemples trois nouveaux cas (deux verts et un rouge) :
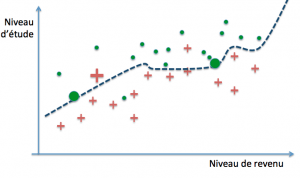
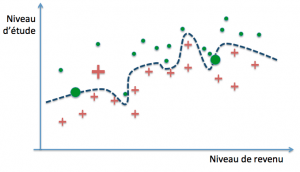
Évaluons l’erreur pour chacun :
Maintenant, réévaluons les paramètres de chacun des trois modèles (ici les coefficients des polynômes) en incluant nos nouveaux exemples dans notre base d’entraînement :

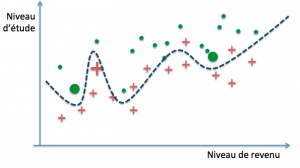
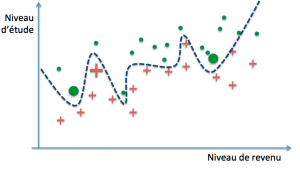
La frontière linéaire n’a pratiquement pas bougé et l’erreur reste la même qu’avant la réévaluation. Dans les autres cas, l’erreur diminue mais au prix d’un changement important de la forme de la frontière de décision : ces modèles sont dits « à forte variance ». Cela signifie que la valeur de leurs paramètres est très fortement influencée par l’ensemble des données d’entraînement.
Regardons de plus près le troisième modèle. Avant le second entraînement, l’accroissement de son erreur sur de nouveaux cas est le plus élevé des trois, et de ce point de vue il ne fait pas mieux que le classifieur linéaire. Ce comportement est symptomatique d’un modèle suradapté à ses exemples d’entraînement.
Ce problème, dit de surapprentissage, est un aspect fondamental du processus d’apprentissage automatisé. En pratique, si l’on cherche à évaluer l’erreur d’apprentissage (commise sur la base des exemples) et l’erreur dite de généralisation (sur des cas de test qui n’en font pas partie), leur évolution aura la forme suivante :
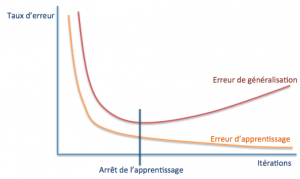
La détermination du point auquel arrêter l’apprentissage est donc cruciale dans la construction d’un modèle ayant de bonnes capacités de généralisation. Certains types de modèles sont plus susceptibles que d’autres au surapprentissage, au point que des techniques spécifiquement adaptées sont parfois intégrées aux algorithmes d’entraînement pour en réduire l’impact.
Une manière plus formelle de présenter le problème est d’exprimer l’erreur en fonction du biais et de la variance : cette relation s’écrit, en français :
Erreur = Variance + Biais2
Tout le problème vient du fait que l’on ne peut pas indéfiniment réduire l’un sans faire augmenter l’autre : l’optimum se situe donc lorsque l’on a réussi à minimiser l’erreur globale. Ce principe est appelé compromis biais-variance et joue un rôle clef dans l’optimisation des modèles.
Comment entraîner un algorithme pour éviter le surapprentissage ?
L’enjeu consiste ici à disposer de jeux d’exemples qui puissent servir à la fois pour l’entraînement et pour l’évaluation de la performance en généralisation. En général, on dispose d’un jeu d’entraînement correctement classé, mais entraîner le modèle sur la totalité des exemples va mécaniquement mener à une situation de surapprentissage. Il s’agit donc de lui réserver des « surprises » afin d’éviter cet écueil.
En pratique, on va procéder à ce que l’on appelle la validation croisée. Cette technique consiste à piocher une portion d’exemples dans l’ensemble d’entraînement et à utiliser la partie restante pour tester le modèle. On itère de la sorte avec des séries d’exemples différentes à chaque fois jusqu’à obtenir la plus petite erreur de généralisation possible.
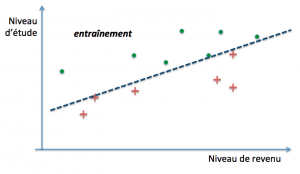
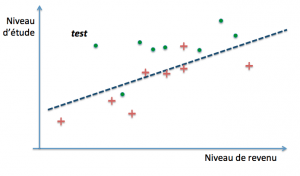
Plusieurs variantes existent. Les plus courantes sont :
Ces méthodes appartiennent pour la plupart à l’une des deux grandes familles que sont les techniques de régression ou de classification. Leur objectif diffère, mais leurs méthodes sont similaires :
Nous explorerons plus avant dans des articles ultérieurs quelques-unes de ces méthodes en détaillant leur fonctionnement dans une situation pratique. Ce qui précède donne une idée du contexte dans lequel elles s’appliquent, et quels sont les grands principes qui les gouvernent.
Nous allons maintenant survoler l’autre versant des techniques d’apprentissage, où le but n’est plus de prédire, mais de découvrir.
L’apprentissage non supervisé a pour but de découvrir des structures dans l’échantillon soumis à son analyse. Pour cela, il va chercher, par divers moyens, à regrouper les individus qui le constituent pour mettre à jour des classes, de manière à faciliter l’explication de l’ensemble. Ce domaine d’étude recoupe une bonne partie des préoccupations que l’on retrouve dans le data mining.
Parmi les problèmes éligibles à un apprentissage non supervisé, on trouve par exemple :
Parmi le panel de techniques existantes, nous allons en citer deux qui sont couramment utilisées : la classification et la réduction de dimensions.
La classification consiste à effectuer des regroupements d’individus par proximité. Deux approches existent pour réaliser cette tâche. La première consiste à partir de l’ensemble des observations et de le scinder en plusieurs classes d’après un critère de distance : c’est le partitionnement. On pourra par exemple choisir de fixer un nombre de classes à l’avance et déterminer autant de regroupements des observations fournies. Par exemple, la figure suivante définit trois regroupements possibles pour 1 (bleu foncé), 2 (rouge) et 4 (bleu clair) classes :
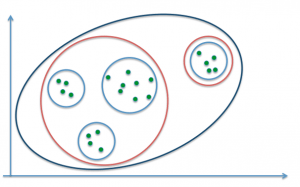
L’approche inverse consiste à démarrer des points individuels et les regrouper successivement en classes de plus en plus grandes : on parle de classification hiérarchique ascendante. On aboutit alors à une arborescence de classes, et il est généralement à la charge de l’analyste de déterminer quelle profondeur de classification est la plus pertinente pour le problème étudié.
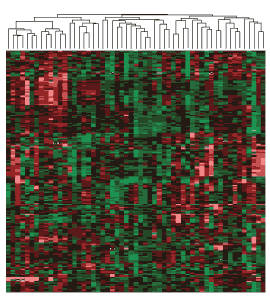
Arbre hiérarchique de classes d’altérations génétiques chez des patients atteints de cancer. La hauteur de « coupe » de l’arbre (figuré au-dessus de la carte) détermine le nombre de classes.
Un second cas d’apprentissage non supervisé concerne la réduction de dimensions. Imaginons que l’on dispose d’un volume d’informations très conséquent, réparti sur un grand nombre de variables, par exemple pour une population humaine l’âge, le poids, la taille, la durée de trajet quotidienne moyenne, le niveau de revenu, le pays de résidence, le nombre d’enfants à charge, la consommation de lait par an… On cherche à déterminer quelles sont les variables les plus explicatives afin de simplifier le problème tout en conservant le maximum d’information. Supposons que nous disposions de trois quantités seulement pour chaque observation, et que nous représentions notre échantillon sur trois axes correspondant. Supposons enfin que les points se répartissent à l’intérieur d’un volume en forme de galet, assez plat et plus long que large :

Si l’on réduit naïvement le nombre de variables en en choisissant deux, par exemple les deux axes du « fond » on perdra une quantité importante d’information sur notre nuage (assimilable à l’ombre portée). En revanche, si on effectue une rotation des axes de manière à « redresser » notre galet, l’information s’en trouve représentée différemment :

Cette rotation des axes revient à construire de nouvelles variables par combinaison des variables originales. Grâce à elles, nous avons une représentation plus « nette » du galet, et nous pouvons choisir de retenir préférentiellement les variables qui représente le mieux notre nuage de points : par exemple, en choisissant de ne retenir que deux variables parmi trois, on pourra choisir successivement le « plancher », puis le « fond » et enfin le « mur de gauche » pour le décrire.
C’est ce que vont rechercher à faire des techniques comme l’analyse factorielle ou l’analyse en composantes principales : trouver des variables composites (des axes) qui portent le maximum d’information, et permettre de n’en garder que quelques-unes pour concentrer l’analyse elles, en considérant la petite perte d’information comme du « bruit » dans la représentation simplifiée ainsi obtenue.
Cette technique trouve son intérêt dans un certain nombre d’applications comme la visualisation de données complexes (typiquement en deux dimensions), la compression avec perte, mais également… la sélection des caractéristiques les plus pertinentes.
Caractéristiques ? Oui, comme dans un problème de classification, par exemple. En fait, il n’est pas rare d’utiliser une passe de réduction de dimension pour faciliter le travail d’un algorithme de régression ou de classification, dont la complexité augmente —parfois très rapidement— avec le nombre de variables.
Nous avons survolé dans cet article les deux principaux volets qui constituent aujourd’hui le champ de recherche de l’apprentissage automatique. Les notions clefs intervenant dans les méthodes d’apprentissage supervisé ou non, comme la régression, la classification, le surapprentissage, l’erreur de généralisation ou la validation croisée devraient paraître un peu moins floues.
Dans les articles qui suivront, nous explorerons plus en détails certains algorithmes en les appliquant à des problèmes concrets. Les notions couvertes ici y seront toujours présentes, au moins en filigrane. Pour ceux qui souhaiteraient les parcourir, le présent article devrait donc éclairer un peu leur lecture.
Et pour rendre les choses plus concrètes, nous commencerons dès le prochain article par confronter un algorithme simple à un problème de classification applicable à la vie courante : le tri de nos relevés bancaires.