“Si j’ai une valeur y qui est fonction de x, comment faire pour déterminer la valeur de x minimisant ou maximisant la valeur de y ?” tel est le problème de base du domaine de l’optimisation, qui se décline à de très nombreux cas d’usage allant de “comment fixer le prix pour maximiser un profit” à “quelle stratégie mon robot doit-il adopter pour rester en équilibre”.
Nous vous proposons dans cet article une introduction aux stratégies d’optimisation bayésienne, un sous-domaine regroupant des techniques très puissantes pour converger efficacement vers des valeurs optimales lorsqu’on fait face à une situation où le nombre d’observations est limité par des contraintes de temps ou de matériel.
Vous souhaitez voir un cas d’usage de ces algorithmes ? Comprendre comment ces derniers fonctionnent et comment les implémenter ? Alors vous êtes au bon endroit. Cet article prend pour exemple la problématique de la configuration automatique des paramètres d’une base de données pour illustrer l’optimisation bayésienne. Nous présenterons un exemple d’implémentation en Python ainsi que quelques autres cas d'usage pour cette approche.
Chez OCTO Technology, nous avons récemment décidé d’explorer des questions de configuration automatique du fonctionnement de bases de données, un domaine particulièrement large mais avec plusieurs problématiques que l’on peut distinguer. L’une d’elles en particulier va nous intéresser ici car elle constitue un bon exemple de situation où l’optimisation bayésienne se révèle pertinente.
Imaginons une base de données, pas nécessairement complexe, avec un ensemble de paramètres à régler : cache, mémoires partagées, nombre de connexions simultanées maximum, etc. Étant donné une charge de travail, tel qu’un ensemble de requêtes exécutées sur cette base de données, on souhaite déterminer automatiquement les valeurs de paramètres qui nous permettront d’obtenir les meilleurs résultats (par exemple, nous voudrions compléter l’exécution de notre charge le plus rapidement possible). Il existe des règles métier fournissant des pistes pour fixer ces paramètres : le site PgTune propose par exemple des configurations pour Postgres en fonction du hardware (RAM, CPU). Mais ces règles ne sont pas forcément adaptées à notre charge de travail, sont rarement optimales et ne s'appuient pas nécessairement sur des théories. Pour résumer, on souhaiterait rendre le choix d’une bonne configuration le plus automatisé et le plus efficace possible mais il est en réalité très difficile de déterminer des règles précises régissant ces paramètres.
Heureusement pour nous, il s’agit finalement d’un problème classique d’optimisation pour lequel de nombreuses solutions existent : nous voulons trouver rapidement une configuration (c’est-à-dire un ensemble de paramètres) maximisant ou minimisant une métrique de performance. Pour cela, nous devons tout de même prendre en compte un certain nombre de contraintes :
Compte tenu de nos contraintes, il est nécessaire de trouver une stratégie d’optimisation pas à pas efficace : nous souhaitons, en un minimum d’observations, déterminer la meilleure configuration. En consultant la littérature académique, nous avons ainsi identifié deux articles explorant également le problème de la configuration automatique d’une base de données : iTuned (2009) et Ottertune (2017). Les auteurs de ces deux publications proposent des solutions similaires basées sur l’optimisation bayésienne afin de rechercher une configuration optimale.
Cette approche séquentielle se trouve être particulièrement adaptée à notre problème de par son principe. L’objectif est d’utiliser un petit nombre d’observations pour estimer un comportement plus global. En exploitant efficacement la connaissance accumulée sur notre fonction boîte noire, on espère minimiser le nombre d’observations et converger rapidement vers la configuration optimale.
Étudions maintenant plus en détail le fonctionnement d’un algorithme d’optimisation bayésienne avant de passer à une implémentation concrète pour répondre à notre problème.
L’optimisation bayésienne est une approche probabiliste basée sur l’inférence bayésienne. En somme, cela veut dire qu'on va chercher à exploiter ce qu’on connaît déjà, donc l’ensemble des événements précédemment observés, pour inférer la probabilité des événements que nous n’avons pas encore observés. Dans le cadre de l’optimisation bayésienne, nous partons d’un ensemble d’observations dont nous connaissons le résultat et nous déterminons pour chaque valeur ???? en dehors de cet ensemble la distribution de probabilité de l’évaluation de ???? en ce point ????.
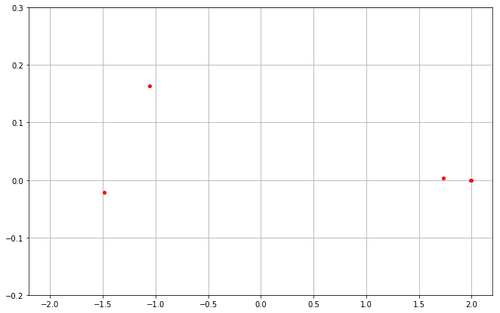
Mais comment calculer cette distribution de probabilité ? Parmi toutes les méthodes existantes, nous retiendrons ici l'une des méthodes classiques qui consiste à utiliser les processus gaussiens qui généralisent le concept de loi normale aux fonctions. Nous ne développerons pas cette méthode un peu complexe. L’important est de comprendre que cette approche nous permet de générer pour chaque point une distribution de probabilité caractérisée par une moyenne µ (la valeur la plus probable) et un écart-type σ (la mesure de la dispersion probable de la valeur autour de la moyenne).
Pour le lecteur souhaitant aller plus loin, cet excellent article de blog développe davantage les processus gaussiens sans aller trop loin dans les détails mathématiques. La publication originale est ensuite la source la plus exhaustive sur le sujet.
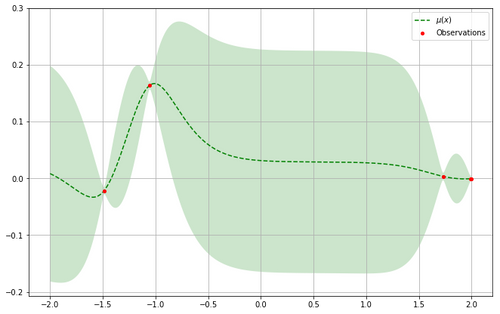
Il est à noter qu’on ne pourra pas représenter cette distribution pour tous les points. Nous ne considérons cette distribution que sur un ensemble fini de points : c’est notre espace de recherche. Ainsi nous aurons, pour chaque point de cet espace de recherche, une valeur centrale, la moyenne μ, et une certaine dispersion autour de cette moyenne, l’écart-type σ. Ce dernier sera d’autant plus faible que l’on sera proche d’un point déjà observé.
Nous sommes à présent capable d’inférer le comportement de notre fonction à partir de nos évaluations. Mais comment choisir quel point évaluer : quel point a les meilleures chances d’être un minimum ?
Rappelons-nous notre objectif : minimiser ou maximiser la fonction observée, c’est-à-dire trouver le point pour lequel l’évaluation est minimisée ou maximisée. Le choix du point utilisé pour l’évaluation suivante est donc soumis à un double critère. Nous voulons d’une part gagner en connaissance sur le comportement de la fonction et donc choisir une zone de l’espace de recherche où l’inconnu est grand : c’est l’exploration. D’autre part, nous souhaitons trouver le point qui minimise/maximise notre fonction : c’est l’exploitation. Ces deux notions sont matérialisées par les indicateurs statistiques cités précédemment que sont l’écart-type et la moyenne. Quand l’écart-type est grand, c’est que la zone est mal connue et donc intéressante à explorer. Quand la moyenne est petite/grande, c’est que la zone observée est intéressante pour trouver un minimum/maximum.
Ce compromis entre exploration et exploitation est exprimé par une fonction d’acquisition. Cette fonction associe à chaque point de l’espace de recherche un potentiel pour être l’optimal. Il existe plusieurs fonctions d’acquisitions, avec des variations subtiles mais gardant le même principe directeur : exprimer le potentiel d’un point.
À chaque étape de notre optimisation, le point choisi pour l’évaluation donc est celui qui maximise notre fonction d’exploitation.
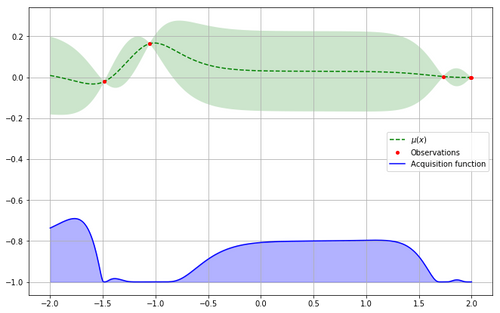
Trouver le nouveau point à évaluer implique donc d’évaluer notre fonction d’acquisition pour tout notre espace de recherche. Cependant ces évaluations seront beaucoup moins coûteuses en comparaison à l’évaluation de la fonction observée. La fonction d’acquisition étant simple et connue, on peut facilement l’évaluer en un grand nombre de points pour trouver le maximum. Le maximum trouvé correspond au prochain point à tester et une fois l’observation réalisée, on peut actualiser notre optimisation avec cette nouvelle information et repartir depuis le début, en répétant jusqu’à converger.
Pour bien comprendre cela, reprenons notre exemple en voyant après plusieurs itérations comment chaque boucle apporte de l’information supplémentaire jusqu’à atteindre un minimum. On peut comparer enfin l’approximation obtenue à la fonction originale (inconnue à la base) à minimiser et vérifier l’efficacité de l’algorithme.
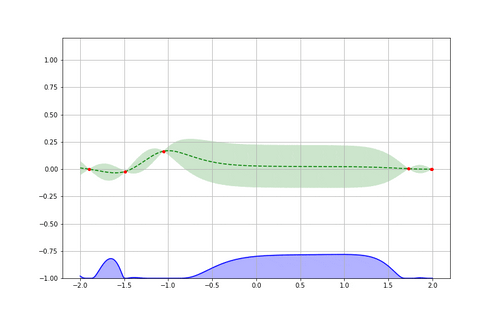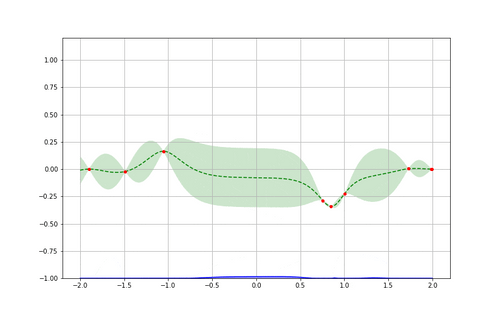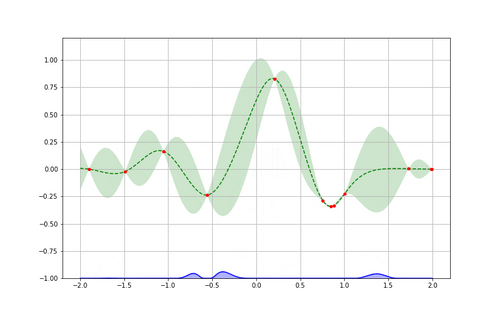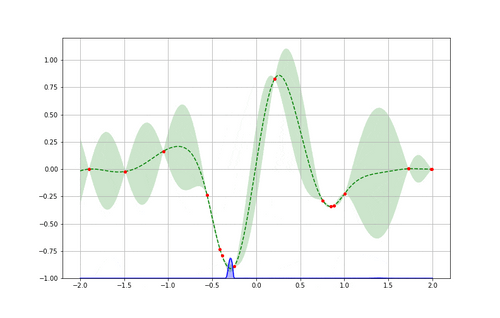
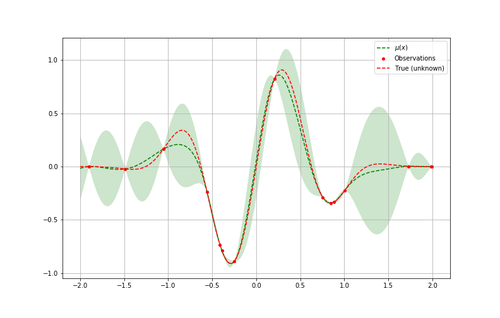
Pour voir cela en pratique, passons à un exemple plus concret !
Maintenant que nous en savons un peu plus sur l’optimisation bayésienne, reprenons notre problème initial et voyons comment implémenter en Python un algorithme répondant à ce même problème.
Supposons une situation où nous souhaitons configurer notre base de données sur laquelle nous pouvons faire varier deux paramètres param_1 et param_2. Le but est de déterminer quelles sont les valeurs de ces deux paramètres permettant de minimiser le temps pour compléter une charge de travail (par exemple un ensemble de requêtes). Les règles métier dont nous disposons ne nous permettent pas de déterminer les valeurs optimales pour ces paramètres et nous fournissent au mieux des bornes dans lesquelles rechercher l’optimum.
Nous allons ainsi utiliser le package Python scikit-optimize (basé sur scikit-learn) pour mettre en place un workflow prenant en entrée un intervalle pour nos valeurs de paramètres et cherchant l’ensemble donnant les meilleurs résultats. Tout le code du workflow et des visualisations est disponible sous forme de notebook Jupyter.
Commençons par définir notre espace de recherche sous forme de dictionnaire :
search_space = {
'param_1': (0.0, 10.0),
'param_2': (0.0, 0.0)
}
Il faut désormais instancier un objet Optimizer, tiré du package scikit-optimize, qui va se charger de la majeure partie du travail. Nous devons préciser à l’Optimizer l’espace sur lequel il va effectuer sa recherche. Comme expliqué précédemment, nous allons utiliser un estimateur basé sur les processus gaussiens (ou Gaussian Process, “GP”).
Pour éviter des effets de bord des processus gaussiens survenant lorsque l’espace des observations est vide (ou quasi-vide), il est aussi préférable de tester les premiers points de manière aléatoire, ce que l’on précise par le paramètre n_initial_points.
opt = Optimizer([search_space['param_1'], search_space['param_2']],
"GP",
n_initial_points=3)
Il n’y a maintenant plus qu’à faire tourner la boucle d’optimisation. La force de scikit-optimize se situe dans la possibilité de faire tourner des workflows relativement asynchrones grâce aux fonctions ask et tell. À chaque étape, nous allons demander (ask) quelle est la configuration qui présente le meilleur potentiel pour pouvoir la tester, c’est-à-dire exécuter notre charge de travail, avant d’obtenir un résultat que nous allons ajouter à nos observations (tell). On boucle ensuite autant de fois que l’on souhaite ou jusqu’à ce qu’un critère de satisfaction soit atteint.
for _ in range(20):
# Quelle est la prochaine configuration à tester ?
next_config = opt.ask() # Renvoie une liste
# Ici, nous avons une dépendance extérieure puisque nous devons mettre à
# jour la configuration de la base de données puis tester notre charge.
# Faisons l'hypothèse que ces interfaces ont été définies ailleurs dans le code.
database.update_configuration(next_config)
runtime = database.benchmark(workload)
opt.tell(next_config, runtime)
Si tout se passe bien, l’optimiseur convergera ensuite naturellement vers un couple de paramètres présentant la meilleure performance.
Pour se représenter cela, supposons que le temps nécessaire pour compléter la charge se comporte de la manière suivante en fonction des paramètres param_1 et param_2 :
L’optimisation bayésienne démontre là tout son intérêt : en un nombre d’observations très restreint (de l’ordre de la dizaine), nous sommes en mesure de déterminer les valeurs des paramètres pour lesquelles notre base de données a les meilleurs résultats. Rapidement, l’algorithme converge vers des valeurs autour de (6, 13) en gardant tout de même un caractère exploratoire pour s’assurer de ne pas être coincé sur un minimum local si le comportement de la base de données avait été plus complexe.
Sur un cas réel, il faut cependant se poser la question du bruit : l’optimisation bayésienne est-elle résiliente lorsque les observations sont bruitées (dans notre cas, on peut par exemple avoir un temps qui varie à cause de perturbations réseaux) ? La réponse est oui, dans une certaine mesure. Sur un cas plus compliqué, disponible sur ce notebook, on voit qu’un niveau de bruit inférieur à 5% peut perturber l’algorithme sans que cela ne soit gênant pour déterminer un minimum rapidement. Un autre exemple sur un espace à une dimension démontre également cela sur le repository du package scikit-optimize.
Lorsque le bruit est plus élevé, il est possible de jouer sur des paramètres qui peuvent prendre en compte l’incertitude (c’est le cas du paramètre alpha de l’estimateur scikit-learn GaussianProcessRegressor). Mais lorsque cette variabilité est trop élevée, l’algorithme ne peut simplement pas fonctionner correctement. Pour cette raison, il est conseillé avant d’utiliser une stratégie d’optimisation bayésienne de vérifier que l’environnement est suffisamment stable et que les observations sont reproductibles. Après tout, on ne peut pas optimiser ce qui varie.

L’exemple précédent d’application de l’optimisation bayésienne est relativement précis, mais la stratégie peut facilement se généraliser à d’autres applications où l’on cherche un ensemble de paramètres maximisant la performance mais que chaque observation est coûteuse.
C’est notamment le cas de la gestion des hyper-paramètres d’un modèle de machine learning, la librairie scikit-optimize est d’ailleurs taillée pour ce type d’utilisation. En effet, lorsqu’on utilise un modèle de machine learning, il est difficile d’évaluer directement la valeur optimale de certains paramètres (par exemple le nombre d’arbres et leur profondeur pour un RandomForestClassifier). Utiliser l’optimisation bayésienne pour résoudre le problème à notre place est tout à fait possible : l’entrée de notre problème correspond aux valeurs des hyper-paramètres et la performance à optimiser est une métrique au choix de l’utilisateur (précision, AUC, etc.).
Cette approche permet notamment de gagner en temps d’optimisation en réduisant le nombre d’observations par rapport à des algorithmes type RandomSearch ou GridSearch qui demandent plus de tests pour arriver à des résultats. C’est d’ailleurs l’approche plébiscitée en 2017 par Google pour le tuning d’hyper-paramètres qui met même en place un système de “hyperparameter tuning as a service” sur Cloud ML.
Convaincu par l’optimisation bayésienne ? Vous souhaitez optimiser rapidement vos modèles de machine learning ? Jetez donc un oeil aux solutions prêtes à l’emploi de librairies Python comme scikit-optimize ou bayesian-optimization qui présentent toutes les deux des exemples d’implémentation appliquée au tuning de modèles ici et ici.
L’approche bayésienne est donc efficace pour répondre au problème du choix de paramètres optimaux lorsque le comportement de la fonction est mal connue, que les observations sont coûteuses et qu’une approche aléatoire ou brute force n’est pas envisageable. Les algorithmes d’optimisation bayésienne se prêtent donc bien à la configuration de systèmes d’informations comme une base de données, à condition de bien connaître son environnement et sa variabilité !
Enfin, on a pu récemment voir de grandes entreprises communiquer sur des initiatives exploitant ces approches. Des ingénieurs de Twitter par exemple, développent un système utilisant l’optimisation bayésienne pour configurer automatiquement et en continu les paramètres JVM de leurs services. En juin 2018, Facebook a présenté Spiral, une librairie destinée à la configuration automatique et temps réel des services avec, en préparation, l’utilisation de l’optimisation bayésienne pour la configuration de paramètres. Autant d’approches illustrant la force de l’optimisation bayésienne lorsqu’on l’applique à la configuration de systèmes informatiques.