Les réseaux de neurones constituent aujourd'hui l'état de l'art pour diverses tâches d'apprentissage automatique. Ils sont très largement utilisés par exemple dans les domaines de la vision par ordinateur (classification d'images, détection d'objets, segmentation…) et du traitement automatique du langage (traduction automatique, reconnaissance vocale, modèles de langage…).
Dans un précédent article, nous avons utilisé une classe particulière de réseaux de neurones, les RNN : Recurrent Neural Networks. Cette famille de modèles, particulièrement adaptée aux données séquentielles, nous a permis de générer automatiquement, caractère par caractère, du texte compréhensible à partir d'une séquence initiale. Nous vous avions alors promis de vous expliquer plus en détail le fonctionnement des modèles en question.
Le but de ce nouvel article est de décortiquer deux variantes de RNN pour en expliquer le fonctionnement interne et démythifier leur aspect "boîte noire". Pour cela, nous utiliserons le même cas d'usage de génération de texte que dans l'article précédent. Il nous servira de fil rouge tout au long de cet article.
Commençons par rappeler le problème de génération de texte. Afin de générer du texte, nous partons d'une séquence de caractères de taille fixe pour prédire le caractère suivant.
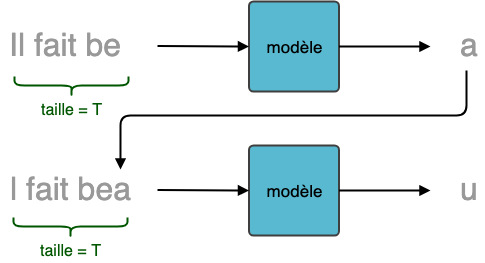
Génération de texte caractère par caractère
Le pré-traitement détaillé dans l'article précédent permet de représenter numériquement le texte brut, le transformant en une matrice dont les dimensions sont nb_échantillons (N) * taille_séquence (T) * nb_variables (M) où :
En résumé, le modèle prend en entrée un tableau de N séquences, chacune de longueur T=10 caractères**,** où chaque caractère est un vecteur numérique de taille M=30.
Une couche de type RNN prend en entrée une séquence de ce tableau (donc une matrice de taille (T x M)) et retourne en sortie un vecteur de taille R qui est une représentation compressée de la totalité de la séquence de caractères. Encore une fois, R est un hyperparamètre à choisir judicieusement. Pour l'exemple, on peut choisir R=16. C'est en quelque sorte l'équivalent du nombre de neurones dans une couche dense (ou "fully-connected").
Traitement d'une séquence de taille T=10 par une couche récurrente
Générer le caractère suivant consiste à choisir le caractère le plus pertinent parmi les M=30 caractères possibles. Il faut donc que notre modèle produise une sortie de taille M=30. Ce vecteur de sortie associe alors à chaque caractère une probabilité d'être le suivant dans la séquence, étant donné les T caractères précédents.
Pour obtenir cette distribution de probabilité, on empile une couche de neurones "classique" (appelée également couche dense) de taille M=30 à la suite de la couche RNN et on utilise une fonction d'activation softmax. Considérons l'exemple ci-dessous: la séquence d'entrée étant "il fait be", la probabilité de sortie la plus élevée pourrait correspondre à la lettre "a", dans l'optique de générer la phrase "il fait beau".
Prédiction de la distribution de probabilité du caractère suivant à partir d'une séquence initiale
Détaillons maintenant ce qui se passe à l'intérieur-même de la couche RNN. Une couche RNN est une succession de T cellules. Chaque cellule a deux entrées :
Une couche RNN, prenant en entrée des séquences de 10 caractères
Dans une couche RNN, on parcourt donc successivement les entrées x1 à xT. À l'instant t, la tème cellule combine l'entrée courante xt avec la prédiction au pas précédent h~t-1 ~ pour calculer une sortie ht de taille R.
Le dernier vecteur calculé h~T ~ (qui est de taille R) est la sortie finale de la couche RNN. Une couche RNN définit donc une relation de récurrence de la forme :
ht = f(xt, ht-1)
La tème cellule n'est rien d'autre qu'une couche dense de taille R, dont l'entrée est la concaténation de xt (de taille M=30) et ht-1 (de taille R). La fonction d'activation classique utilisée pour les cellules du RNN est la tangente hyperbolique tanh. Plusieurs propriétés intéressantes expliquent ce choix, notamment une convergence plus rapide que la sigmoïde.
Zoom sur une cellule de RNN
La formule devient donc:
ht = tanh( WT * concat (xt, ht-1) + b )
où W et b sont les poids appris par le modèle :
Il est à noter que les poids sont partagés entre toutes les cellules d'une couche RNN. Autrement dit, c'est exactement la même fonction (avec les mêmes poids) qui est appliquée à chaque pas de temps t. Cela permet à la fois de modéliser toute la séquence de façon homogène et d'éviter de multiplier le nombre de poids à apprendre. En effet, si on apprenait une matrice de poids différente pour chacune des T cellules, il faudrait alors apprendre T matrices (W1,..., WT) au lieu d'une seule.
Selon les implémentations, il est possible que la matrice W soit séparée en deux parties :
C'est notamment le cas dans la librairie Keras que nous utilisons. Le code ci-dessous permet de définir un modèle simple à 1 couche RNN, où R=16, qui prend en entrée des séquences de taille T=10 caractères, chacun encodé comme un vecteur de taille M=30.
from keras.layers import SimpleRNN
model = Sequential()
model.add(SimpleRNN(units=16, input_shape=(10, 30), use_bias=False))
On voit alors que notre modèle a 736 paramètres (ou poids) à apprendre.
print(model.summary())
_________________________________________________________________
Layer (type) Output Shape Param #
========================================================
simple_rnn_1 (SimpleRNN) (None, 16) 736
========================================================
Total params: 736
Trainable params: 736
Non-trainable params: 0
_________________________________________________________________
On peut même récupérer les formes des matrices de poids apprises par le modèle.
print([weight_matrix.shape for weight_matrix in model.get_weights()])
[(30, 16), (16, 16)]
Dans notre cas, on peut constater que le modèle apprend 2 matrices de poids:
Dans la suite de l'article, et par souci de simplification, on représentera de façon condensée une cellule RNN de la façon suivante:
Représentation simplifiée d'une cellule RNN
Souvent, une seule couche RNN ne suffit pas à capter toute l'information contenue dans les séquences. On peut alors empiler les couches de type RNN afin d'avoir un réseau plus profond, comme on le fait couramment avec des couches denses ou convolutives. Cela permet d'extraire des informations plus complexes à partir des entrées, et ainsi d'avoir une meilleure modélisation de nos données.
Dans la plupart des cas, 2 ou 5 couches récurrentes suffisent; au-delà, la convergence devient difficile. Cette "faible" profondeur est en réalité trompeuse, car les couches RNN sont en quelque sorte profondes par construction, vu qu'une couche unique traverse itérativement de longues séquences.
Essayons de construire un réseau à 2 couches récurrentes. La première couche RNN retourne un vecteur unique h1T de taille R. La deuxième couche, elle-même récurrente, a besoin d'une séquence de vecteurs en entrée, et non d'un vecteur unique.
Comme fait-on alors pour satisfaire cette condition ? La solution consiste à donner en entrée de la couche 2 la séquence des sorties intermédiaires h11, h12, ..., h1T de la couche 1, et pas seulement la sortie finale. Le schéma de notre modèle est alors le suivant :
Empilement de deux couches de RNN
On peut implémenter un tel modèle avec Keras de la façon suivante :
model = Sequential()
model.add(SimpleRNN(units=16, input_shape=(10,30), return_sequences=True))
model.add(SimpleRNN(units=4))
On peut remarquer dans le code ci-dessus que l'hyperparamètre "units", qu'on a noté R dans notre article, peut être différent d'une couche à l'autre.
Bien qu'ils soient construits spécifiquement pour gérer des séquences, les RNN simples ont certaines limites.
Une couche RNN est une succession de cellules, chacune prenant en entrée la représentation du caractère courant ainsi que la sortie de la cellule précédente (c.f schéma paragraphe 2.A). Ces données d'entrée sont transformées, en passant notamment par une fonction tangente hyperbolique.
La tangente hyperbolique a tendance à écraser les valeurs qu'elle prend en entrée. En effet, elle est définie sur l'espace des réels mais ses valeurs de sortie sont dans l'intervalle ]-1, 1[. Ainsi, après un premier passage par la tangente hyperbolique, on obtient une valeur entre -1 et 1. Ensuite, comme tanh(1) = 0.76 et tanh(-1) = -0.76, un deuxième passage par la fonction tanh résulte en un intervalle de valeurs encore plus réduit, et ainsi de suite.
Comparaison des courbes des fonctions tanh et de ses compositions successives
Les informations provenant de x1 passent T fois à travers une tangente hyperbolique, là ou celles provenant de xT subissent cette transformation une seule fois. Cet effet d'écrasement aurait pu être compensé par un poids plus fort associé à h1, via la matrice de poids W. Cependant, comme cette matrice est partagée par toutes les cellules de la couche, toutes les sorties intermédiaires sont pondérées par les mêmes poids. Intuitivement, l'influence de x1 dans la prédiction sera donc plus petite que celle de xT. Dès lors, même si x1 est cruciale pour la tâche de prédiction, son influence est mécaniquement réduite par les passages successifs par la tangente hyperbolique.
Prenons un exemple pour comprendre en quoi cela peut être problématique. Supposons que notre séquence en entrée est “il prévien". Pour prédire la prochaine lettre, qui correspond à l'accord du verbe, il est nécessaire de connaître le sujet. Or, cette information se trouve en début de séquence. Le modèle aura potentiellement du mal à différencier cette séquence d'une autre qui lui ressemble: "tu prévien". Il pourrait donc donner une haute probabilité à un "s", et ainsi se tromper. Ce problème devient très embêtant lorsqu'on utilise des séquences plus longues, il est donc très compliqué pour un RNN basique de générer un texte cohérent dans la longueur.
L'une des principales difficultés pour entraîner des réseaux de type RNN est le problème du vanishing gradient. Pour comprendre ce problème, faisons tout d'abord quelques rappels au sujet de l'entraînement d'un réseau de neurones. Un réseau de neurones est un enchaînement de fonctions simples, prenant en entrée les données de notre problème X. Dans notre exemple de génération de texte, il s'agit des N séquences de taille T.
Cet enchaînement de fonctions a comme paramètres des poids W. L'apprentissage consiste à ajuster les poids W afin de minimiser une erreur, donnée par une fonction de coût L. Cette erreur mesure l'écart entre les labels réels y (la "vérité", les caractères que le modèle est censé prédire) et les labels prédits ŷ (les caractères prédits par le modèle). Elle est mesurée sur une partie de nos données (Xtest, ytest).
L'entraînement a lieu comme il suit :
Un réseau de neurones est une suite de fonctions (couches) appliquées successivement. Calculer son gradient revient donc à dériver des fonctions composées. Schématiquement, cela revient à calculer la dérivée d'une fonction composée comme une multiplication de dérivées partielles des fonctions qui la composent.
Ainsi, si notre modèle est composé de trois couches et est représenté par la fonction f ∘ g ∘ h, son gradient par rapport à W sera df/dg * dg/dh * dh/dW.
Dans le cas d'une couche RNN, on a :
avec fW(x, h) = tanh(WT concat(x, h) + b) et une fonction de coût L(h3, y).
Le gradient de h3 par rapport à W est donc proportionnel à la multiplication de dérivées de la fonction tangente hyperbolique. Or, la dérivée de cette fonction se situe dans l'intervalle [0, 1] et prend presque sûrement des valeurs dans [0, 1[.
Courbe de la dérivée de tanh
Or, plus on multiplie des valeurs entre 0 et 1 entre elles, plus le résultat se rapproche de 0. dL/dW prend donc des valeurs très petites lorsque les séquences sont longues. La mise à jour des paramètres devient donc très lente et l'entraînement du modèle est mis à mal.
Plusieurs variantes aux RNN standards ont vu le jour pour remédier aux problèmes évoqués précédemment. Nous allons ici décrire les LSTM, pour Long Short-Term Memory. Ce type de RNN est très utilisé en traitement du langage naturel.
L'idée derrière ce choix d'architecture de réseaux de neurones est de diviser le signal entre ce qui est important à court terme à travers le hidden state (analogue à la sortie d'une cellule de RNN simple), et ce qui l'est à long terme, à travers le cell state, qui sera explicité plus bas. Ainsi, le fonctionnement global d'un LSTM peut se résumer en 3 étapes :
Pour un autre exemple illustrant l'intuition derrière les LSTM, voir cette discussion sur Quora.
Regardons cela de plus près. En respectant la même convention que pour le schéma simplifié de la cellule RNN, on peut représenter une cellule LSTM de la façon suivante :
Représentation simplifiée d'une cellule LSTM
Comme le RNN, le LSTM définit donc une relation de récurrence, mais utilise une variable supplémentaire qui est le cell state c :
ht , ct = f(xt, ht-1, ct-1)
L'information transite d'une cellule à la suivante par deux canaux, h et c. À l'instant t, ces deux canaux se mettent à jour par l'interaction entre leurs valeurs précédentes ht-1 et ct-1 ainsi que l'élément courant de la séquence xt.
Dans le paragraphe suivant, nous allons essayer de comprendre pas à pas les opérations réalisées par une cellule LSTM. Les schémas suivants sont inspirés de l'excellent article de C. Olah.
1 - La tème cellule LSTM prend 3 vecteurs en entrée :
C'est ce dernier vecteur que nous allons suivre particulièrement. Il s'agit d'une route privilégiée de transmission d'information sur la séquence. Pour éviter le problème du vanishing gradient, le cell state est en effet mis à jour de façon additive à chaque étape, sans passer par une activation.
Entrées d'une cellule LSTM : input, hidden state, cell state
2 - La forget gate est une couche dense de taille R avec une activation sigmoïde. À partir de ht-1 et xt, cette forget gate produit un vecteur ft de taille R, dont les valeurs sont comprises entre 0 et 1.
Filtre de la forget gate
3 - La forget gate agit comme un filtre pour "oublier" certaines informations du cell state. En effet, on effectue une multiplication terme à terme entre ft et ct-1, ce qui a tendance à annuler les composantes de ct-1 dont les homologues côté ft sont proches de 0. On obtient alors un cell state filtré, toujours de taille R.
Cell state filtré par la forget gate
4 - L'input gate produit un filtre it de valeurs comprises entre 0 et 1 et de taille R, à partir de ht-1 et xt, de façon similaire à la forget gate.
Filtre de l'input gate
5 - En parallèle, un vecteur kt de taille R est créé par une couche tanh. kt est le vecteur candidat pour mettre à jour le cell state.
Vecteur candidat à la mise à jour du cell state
6 - Le candidat kt est filtré par l'input gate it via une multiplication terme à terme. On obtient le vecteur de mise à jour du cell state.
Vecteur candidat filtré par l'input gate
7 - Le cell state filtré (obtenu à l'étape 3) est mis à jour grâce au vecteur candidat filtré (obtenu à l'étape 6). La mise à jour est une simple addition terme à terme de ces deux vecteurs. On obtient alors le nouveau cell state ct.
Mise à jour du cell state par addition du vecteur candidat filtré
8 - De façon analogue à ft et it, l'output gate produit un filtre ot de valeurs entre 0 et 1, et de taille R.
Filtre de l'output gate
9 - Les valeurs du nouveau cell state ct sont ramenées à l'intervalle ]-1, 1[ par une activation tanh. Un filtrage par l'output gate ot est ensuite effectué pour enfin obtenir la sortie ht.
Nouveau hidden state
Des recherches sur les architectures RNN pour les tâches de traduction ont démontré que le sens de lecture classique des séquences n'est pas optimal. En effet, ils ont montré empiriquement que lire les séquences à l'envers améliore significativement la performance du modèle dans ce genre de problèmes. La combinaison des deux sens de lecture (bidirectional RNN) donne des résultats encore meilleurs. Ce dernier résultat est prévisible, vu qu'une représentation bidirectionnelle permet au modèle d'accorder autant d'importance aux premiers caractères de la séquence qu'aux derniers. La version unidirectionnelle, quant à elle, "dilue" mécaniquement les premiers caractères, même si ce phénomène est moins prononcé dans un LSTM que dans un RNN simple.
À travers cet article, nous avons tenté d'expliquer le fonctionnement interne des RNN, et d'une de leurs variantes les plus utilisées, le LSTM. Ces structures, construites pour traiter des données séquentielles, sont à la base de grandes avancées en NLP, que ce soit pour la modélisation du langage, la traduction ou le résumé automatique de texte.
Bien qu'efficace, cette approche a quand même quelques inconvénients. L'un des défauts des LSTM est qu'il est nécessaire de lire entièrement une séquence pour produire une prédiction. En traduction par exemple, cette démarche reviendrait à lire entièrement une phrase en mémorisant tous ses mots, pour ensuite produire une phrase traduite d'un seul coup. On imagine mal un humain procéder de la même façon.
Les architectures utilisant le mécanisme d'attention répondent à cette limitation des LSTM. Elles suivent l'intuition que tous les mots n'ont pas le même poids sémantique dans la production d'une phrase traduite, et qu'on ne traduit jamais mot à mot. En se focalisant sur des parties de la phrase, et en identifiant un contexte "utile" pour chaque mot, ces mécanismes permettent d'améliorer encore plus les performances des modèles.
Lors de notre prochain article, nous analyserons certains modèles d'attention et tâcherons d'expliquer leur apport en NLP.