Nous allons présenter dans cet article le filtre de Bloom, une structure de données méconnue mais appréciée, tant pour sa simplicité d’utilisation que pour les gains de performance qu’elle permet d’apporter.
Elle a été choisie par l’équipe de Google Chrome pour implémenter la fonctionnalité « Safe Browsing » qui protège les utilisateurs contre des attaques de fishing et contre certains types de malware. Avec Safe Browsing, le navigateur effectue une validation avant de commencer le chargement d’une page. Si l’URL en question est identifiée parmi une vaste blacklist, Chrome affiche une alerte à l’utilisateur.
Le stockage de cette blacklist pose problème, à cause de son volume. Un million d’URL représentées de manière classique occuperaient environ 30MB, soit l’équivalent de l’empreinte mémoire totale du navigateur.
Chrome a choisi de représenter cette liste sous la forme d’un filtre de Bloom, ce qui a permis de réduire la consommation mémoire à deux mégas, et de garantir une validation en temps constant.
Cet article va détailler l’implémentation d’un filtre de Bloom, expliquer ses propriétés principales et proposer plusieurs scénarios d’utilisation concrets.
Le filtre de Bloom est une structure qui permet de savoir si un élément est inclus dans un Set, en temps constant.
Il est implémenté par un bitfield de taille constante, couplé à des algorithmes d’insertion et de requête. Il obéit à plusieurs lois qui le différencient d’un Set classique, notamment des lois de type probabiliste.
Règles de base:
Deux paramètres conditionnent le dimensionnement:
Exemples de consommation mémoire:
La consommation mémoire dépend linéairement du nombre de clefs et logarithmiquement du taux d'erreurs. Elle ne dépend pas de la taille des clefs :)
Il existe un autre paramètre, la liste de fonctions de hachage. On en parlera plus tard mais l'utilisateur final de la librairie n'a pas besoin de l'avoir en tête.
Une bonne classe python vaut mille mots.
class BloomFilter:
# Constructeur
def __init__(self,capacity,errRate):
# Dimensionnement du filtre
self.k,self.N = bloom_size(capacity,errRate)
# Bitfield de taille N
self.bitfield = [0] * self.N
def add(self,key):
for n in makeHashs(key,self.k,self.N):
self.bitfield[n] = 1
def contains(self,key):
hashs = makeHashs(key,self.k,self.N)
return all([self.bitfield[n] == 1 for n in hashs])
Le constructeur calcule les besoins du filtre et alloue un bitfield (dans un tableau standard pour simplifier cette implémentation). Le membre self.N est la taille du bitfield en mémoire. Self.k est le nombre de bits qu’on insérera pour représenter chaque clef.
La méthode add ajoute une clef au filtre. Elle calcule une série de hashs , isomorphes à des indices dans le bitfield, modulo N, puis les positionne tous à 1.
La méthode contains nous dit si le filtre reconnait une clef. Il calcule la même série de hashs et examine le bitfield. Si tous ces bits sont à 1, alors on dit que la clef a été trouvée.
Les fonctions de hachage sont cruciales dans une bonne implémentation du filtre de Bloom. Elles doivent être statistiquement indépendantes et uniformes, au risque d’entraîner un excès de collisions et donc de faux positifs. Voici une implémentation correcte, basée sur l'algo SHA1.
Pourquoi SHA1 ? Parce que c’est un algo de hachage cryptographique. Tous les algos de cette famille génèrent des nombres pseudo-aléatoires, répartis uniformément sur l’intervalle de sortie, et donnent la garantie que deux clefs différentes produiront des valeurs indépendantes, au sens statistique.
Ces deux garanties nous disent donc que SHA1(x) est indépendant de SHA1(x+x) et de SHA1(x+x+x) etc... On prendra ces k valeurs, modulo N.
import hashlib
# Fabrique une liste de n hashs basés sur SHA1.
# Chaque hash est un entier entre 0 et max-1
# Cette fonction simule la création de n fonctions différentes (la base théorique du filtre # de Bloom) en renvoyant n valeurs "suffisamment indépendantes".
def makeHashs(key,n,max):
res = []
m = hashlib.sha1()
# On sérialise la clef pour rendre la
# fonction makeHashs polymorphique.
s = str(key)
for i in range(n):
m.update(s) # Et on re-hache la même valeur
hash = int(m.hexdigest(),16) % max
res.append(hash)
return res
Regardons enfin la fonction de dimensionnement. La taille N du bitset est O(nombre de clefs) et O(log(errRate)):
import math
# Calcule un dimensionnement correct (nombre de hashs, taille du bitset) pour un filtre de Bloom
def bloom_size(capacity,errRate):
factor = math.log(1/(math.pow(2.0, math.log(2.0))))
N = math.ceil((capacity * math.log(errRate))/factor)
k = math.ceil(math.log(2.0) * N / capacity)
return int(k),int(N)
C'est tout! L'implémentation est très simple. Testons cette nouvelle librairie dans une session interactive, pour clarifier tout ce qui n'était pas évident jusqu'ici.
>>> b = BloomFilter(5,0.1)
>>> print b.N
24 # on va utiliser un bitfield de 24 bits
>>> print b.k
4 # on va calculer 4 hashs entre 0 et 23 pour chaque clef
>>> b.add("premiere clef")
>>> print b.bitfield
[0,0,0,0,1,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0]
# Les 4 hashs de la 1ere clef
b.add("deuxieme clef")
>>> print b.bitfield
[0,0,0,0,1,1,1,0,0,0,0,1,1,0,0,0,1,0,0,0,0,0,0,0]
# Les 2 nouveaux bits (+ 2 "collisions", ça arrive de temps en temps!)
>>> b.contains("deuxieme clef")
True
>>> b.contains("troisieme clef")
False
La première règle du filtre (« on peut ajouter mais pas retirer ») est illustrée ici. Après l’insertion de la deuxième clef, on ne pourra plus retirer sa « signature » sans retirer deux des quatre bits issus de la première clef.
Une nouvelle propriété intéressante émerge de cet exercice : il est possible de calculer l’union de deux filtres de Bloom en faisant un OU binaire sur leurs bitfields respectifs.
Corollairement, il est possible de synchroniser deux filtres en n’appliquant que le diff du filtre enrichi. Comme ce diff est dense en 0, il est facile à compresser. C’est la méthode utilisée par Google Chrome pour synchroniser le filtre de mon navigateur avec la liste officielle.
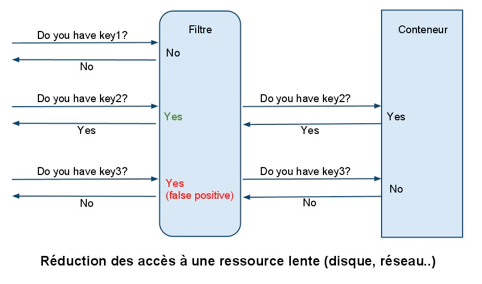
On retrouve des filtres de Bloom dans des applications très diverses. Souvent d’une manière transparente, quand ils constituent une simple optimisation, parfois d’une manière plus évidente, quand ils rendent l’application possible.
Dans la catégorie optimisation, on peut schématiser le pattern de réduction du nombre d’accès à une ressource lente via un cache (voir ci-dessus).
Et voici deux applications qui auraient été impossibles sans un filtre de Bloom :
On pourrait aussi imaginer quelques utilisations nouvelles :
Le filtre de Bloom fournit un moyen économique de représenter de grands ensembles de données, avec des garanties de performance intéressantes. Il permet, au prix d’un peu de mémoire, d’accélérer considérablement certaines applications.