Graphs are very attractive when it comes to modelling real-world data, because they are intuitive, flexible (more than tables and rows in a RDBMS), and because the theory supporting them has been maturing for centuries. As a consequence, there are several graph databases available, Neo4j being one of the most renowned.
The same goes for graph processing, algorithms are numerous and well understood and have immediate applications: single-source shortest path, route finding, loop detection, subgraph matching, ... to name a few. Neo4j comes with a small collection of such algorithms built in its graphalgo package.
Problems arise when processing very large graphs, when visiting billions of highly connected vertices. In such cases a graph can’t fit on a single machine, and the implementation resorts to a big batch distributed over a cluster of machines. Algorithms typically follow the edges of the graph, so a naïve approach will introduce significant overhead due to machine-to-machine communication (partitioning the graph optimally across the cluster is little more than partitioning the graph without heuristics, a hard problem).
We will give an overview of the use of BSP (Bluk-Synchronous Parallel), an algorithm often used for processing of such large graphs. Then we will explore a list of products and frameworks dedicated to graph processing, either using BSP or based on other approaches.
NB: to prevent ambiguities, in the following an element of a graph will be coined a “vertex” or an “edge”, while a “node” will refer to a computation unit in a cluster of machines.
An answer to problems arising with very large graphs is the Bulk-Synchronous-Parallel (BSP) algorithm. It is not an algorithm derived from graph theory; in its most general form it doesn’t even deal with graphs.
Rather, BSP is to be compared to MapReduce: it is a way of distributing the batch processing of a big dataset across a cluster of machines. The difference lies in the flow of data that is exchanged as the processing takes place. MapReduce shuffles batches of independent records, according to a partition scheme reflecting the topology of the cluster, to achieve data and computation colocality. In order to enforce this locality, data is merged and shipped as it enters map or reduces phases, which is costly.
Instead, BSP partitions the input data once and for all during its initialization phase, and each node processes its subset of the data (partition) independently by consuming messages from a private inbox: the data does not move from node to node, rather nodes exchange instruction messages that are assumed to be small and thus more efficiently transmitted. This is an incarnation of the Message Passing Interface (MPI) pattern.
There is no restriction on the outcome of the processing phase: modification of the local partition’s data, output of a new data set, ... and in particular production of new messages, which will be shipped to the appropriate nodes and consumed on the next iteration, and so on. A master node ensures that all nodes have finished processing the current iteration before firing the next one – such iterations are called supersteps.
Thus after each superstep, all nodes join a common synchronization barrier. The role of this barrier is to decouple the production and consumption of messages: all nodes pause their activity while the BSP plumbing enqueues messages into each node’s private mailbox, ready for consumption when processing resumes at the next superstep. This way a message produced by node A for node B will not interrupt the latter during its processing activity. Resources are mostly dedicated to computing, and each node can run its processing routine without concern about concurrent access to the data it owns (no locks needed, unless of course the routine itself is multithreaded). As a downside, the barrier may hinder the whole batch if the processing is not equally balanced between nodes: faster nodes will sit idle while waiting for the other ones to complete a superstep.
The algorithm ends when no messages are produced during an iteration.
In the description of the BSP algorithm, there is no mention of a graph, no restriction on how input and output data are represented. When the input data set is a graph, though, BSP is a sensible approach. This is the direction Google took in the implementation of Pregel, as discussed in their 2010 paper, which we strongly recommend you to read. Pregel is both a BSP implementation and a graph processing library on top of it.
The idea behind Pregel is that many massive graph processing algorithm consists in exploring the graph along its edges. Starting from a fixed set of vertices, one can hop from vertex to vertex and “propagate” the execution of the algorithm, so to speak, across the set of vertices. This reminds of BSP’s way of running an algorithm iteratively by passing messages. In BSP messages are exchanged between computation nodes, in Pregel messages are exchanged between vertices of the graph. Knowing the partitioning function of the graph, it’s easy to know what node hosts each vertex so that each node can dispatch incoming messages at the finest level:
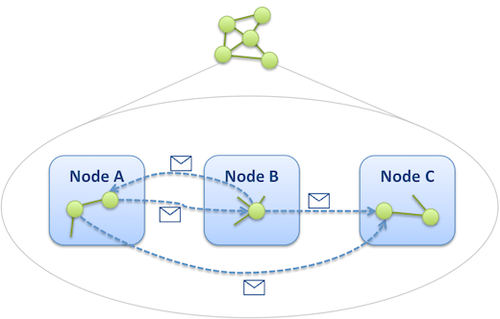
In Pregel the logical level we mentioned earlier takes the form of a vertex-centric C++ API designed around an abstract Vertex class. Once the graph is loaded into the cluster, all processing occurs in memory. Each vertex exposes an ID that is used for both partitioning and message addressing. Concrete classes also define custom attributes so that each vertex instance bears its own properties. They provide an implementation for the Vertex::Compute() function, that implements the intended algorithm – the function can alter attributes of the vertex, address new messages to other vertices (e.g. by enumerating the outgoing edges of the vertex), or even modify the topology by creating and deleting other vertices or edges. The Compute() function receives, as an argument, the list of messages that were sent to the vertex during the previous superstep.
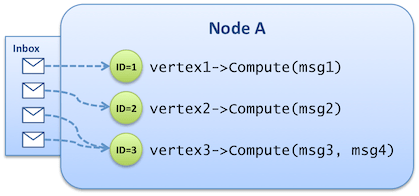
We mentioned that the graph itself can be modified during processing. That is, vertices or edges can be added or deleted. The modifications are applied between supersteps, at the same point where messages are exchanged, so that the user code executing a given superstep doesn’t need to protect itself for modifications in the middle of its execution. Automatic and user-provided strategies apply when several pending modifications are in conflict (e.g. adding an outgoing edge to a vertex being deleted).
What about fault tolerance? The system needs to be able to recover from a node crashing. In Pregel, according to the paper at least, fault tolerance is not enforced by processing each partition redundantly on several nodes; rather, each node regularly performs a checkpoint by flushing its working set to disk. The coordinator node then has all remaining nodes resume processing at a point in time compatible with the complete set of checkpoints saved by each one.
Just as with MapReduce again, several teams took inspiration from the Pregel paper and started to write their own implementations, or at a minimum refer to Pregel as a basis for comparison with their own approach. And, of course, Pregel is not available to the public. Here is a quick survey of the most visible alternatives.
HAMA is one of the most well-known Pregel “clones”. According to Edward J.Yoon, the project leader, HAMA is about to end its incubating period and become a top-level Apache project.
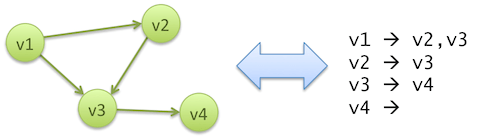
Actually it’s not a Pregel clone; HAMA started in 2008, 2 years before the Pregel paper was issued. It is a BSP implementation over Hadoop, with a small graph processing framework atop that is inspired by Pregel. Vertex data comes in and out of Hama through HDFS APIs, in the form of adjacency lists stored in text files: each line begins with a vertex ID, followed by the list of IDs of vertices connected to the former by its outgoing edges.
The upcoming 0.5.0 release will rely on Hadoop 1.0, but the set of functionalities that will be added is not detailed. All we can say from the source code for 0.5.0-RC2, is that there doesn’t seem to be any built-in connector (for HBase or Neo4j for example), and that the Pregel-like API will not be 100% complete (no aggregators or explicit support for topology mutations). Still, this will have to be confirmed when 0.5.0 is released.
Another incubating Apache project, Giraph (started in 2010), directly took the Pregel path. It features a single release, 0.1.0 (Feb 2012), based on Hadoop 0.20. The PageRankBenchmark example included runs fine on Hadoop 1.0.2, provided the project is recompiled against the appropriate version of the libraries.
The Giraph API, as far as one can tell, is closer to Pregel’s and more complete in this respect, since the project was explicitly started as a clone. Regardless, Hama and Giraph are quite close to each other in their approach – Hama is more mature with several releases, but Giraph has active contributions from Yahoo!, Facebook, Linked and Twitter employees, so watch out. In terms of technologies, both products rely on the same Hadoop components to manage a cluster of graph processing nodes (Hadoop and Zookeeper for job management and synchronization, RPC for message delivery, HDFS APIs for data input and output).
According to this presentation, Giraph mimics Pregel’s strategy of issuing checkpoints for fault tolerance, but how exactly is not clear since the documentation is still a bit scarce...
This project is mentioned here because it’s also stated as a “Pregel implementation”. Phoebus is written in Erlang.
As what seems to be a single developer’s hobby project, its future is uncertain – though commits are still being brought to the code base. It’s certainly not ready today for production use, because the README file has been announcing fixes for fault tolerance since day 1.
GoldenOrb is yet another Pregel clone, or used to be. As a matter of fact, a single version – 0.1.1 – was released in Aug 2011, and the source code has been showing no activity ever since. Besides, it was supported by Ravel Data, a company that is probably out of business (its website is down).
The projects listed below are not Pregel clones or BSP implementations, and advertise themselves as graph processing platforms among other things.
Still, with the exception of Haloop, they have one thing in common: like BSP, they rely on message passing between vertices in order to propagate the processing along the graph. Often they try to compare themselves to Pregel. Another common feature between these projects is their academic nature.
HipG is founded by VU University in Amsterdam. The 1.5 and 2.2 versions, released in early 2011, can be downloaded directly from the website (source code is available but there is no public source control).
HipG is a Java-based distributed processing framework, relying on a message-passing framework from Ibis. HipG features a graph API quite close to Pregel’s, but the core algorithm is finer-grained than BSP, as there is no single synchronization barrier and thus no global supersteps.
Of course, by defining a single barrier one can simulate BSP, but other algorithms can be made more efficient with a hierarchy of barriers conducting a tree of dependent processing tasks (see the HipG paper, section 2.3). In contrast, with BSP several nodes can sit idle waiting for other nodes to complete the current superstep, even if they are dealing with a completely independent portion of the dataset.
Although HipG is distributed in nature, fault tolerance is not implemented yet, as stated in the conclusion of the paper.
Signal/Collect is another academic project, founded by the University of Zurich and Hasler Stiftung (Swiss foundation for the promotion of IT). As BSP and Pregel, it uses the MPI paradigm to process the graph, and supports both synchronous (= BSP) and asynchronous (= actors) models. In contrast with other solutions that are strongly vertex-centric (the Pregel influence, again?), the Signal/Collect API gives vertices and edges the same importance.
Signal/Collect is written in Scala. The latest release, 1.1.2 (Mar 2012), doesn’t support distributed processing, but this is announced for the 2.0 version due in May 2012. Distribution will be implemented with Akka, so 2.0 will probably be a major rewrite of the project.
Trinity paper published by Microsoft.
The first obvious differences with Pregel and other processing frameworks, is that Trinity is a processing engine and a graph database (itself built on top of a key/value “memory cloud”, as they coin it). The approach is not BSP, but relies on vertex-to-vertex message passing without the cost of a global synchronization barrier. Trinity is meant to address both offline analytics and online querying – with the perfomances claimed, such online querying doesn’t limit itself to CRUD access to the database, but also covers heftier processing such as searching 3-hop friends in a social network.
In order to achieve this performance, several techniques are applied. First, as a necessary condition, all processing occurs in memory. The set of vertices necessary for a given computation stage is kept compact, to keep the number of computation nodes low and save on bandwidth (the paper claims “dozens” of servers, as opposed to the “hundreds” or “thousands” of Pregel and such, but the discussion lacks argumentation since the actual uses of Pregel at Google are not known).
Another interesting factor concerns the partitioning of the graph. In addition to the traditional partitioning across the cluster, Trinity makes the sensible assumption that most messages will be sent along the edges of the graph. This heuristic is used to perform a second, orthogonal partitioning, reflecting the vertices and the nodes that are most likely to communicate together. The combination of the two schemes is called bipartite partitioning. It eliminates the need of BSP’s global synchronization barrier, because Trinity can tell when a vertex has received all its messages in the current iteration, without waiting for all nodes to join a common barrier. The heuristic raises an interesting question, unanswered in the paper: can the processing algorithm modify the graph on the fly? Modification of vertex attributes is permitted, but I doubt the topology can be modified as it directly impacts vertex placement and the optimization of message delivery.
Regarding the API, it is quite different than Pregel’s. Vertices do not expose a single Compute() method, rather each vertex go through a pipeline of independent processing stages. “Cell parsers” take care of transforming vertices between stages, eliminating unnecessary local variables to keep the graph compact in memory.
The project advertises itself as a prototype on its front page, so don’t expect production-ready code. It is supported by the National Science Foundation.
Haloop takes a different approach than the other frameworks. It is not a BSP implementation, nor is it built on top of an MPI core: Haloop enhances Hadoop by allowing iterative jobs (loops). Of course, BSP can be approximated by writing a big outer loop called superstep, but the flow of data would still be that of Hadoop.
Haloop is actually a fork of Hadoop 0.20.x. There is no official release, but the source code is publicly available under an Apache 2.0 license.
Provided your use case deals with a large graph, or your problem can be modelled as a graph before being stuffed into a processing service, the following table should help you decide which products should be considered as eligible for your needs.
Pregel is identified by almost all projects as the reference for distributed processing of large graphs, so we tried to show how much of the Pregel API is proposed by the various solutions.
| Project | Type | Algo / Approach | Pregel-like API1 | | | | Fault tolerance | Stack | Recent activity | License | | --- | --- | --- | --- | | | | --- | --- | --- | --- | --- | --- | --- | | V | A | C | M | | Hama2 | Incubation3 | BSP | Y | N | Y | N | Y | Hadoop 1.0 | Active | Apache | | Giraph | Incubation | BSP4 | Y | Y | Y | Y | Y | Hadoop 0.205 | Active | Apache | | Pheobus | Hobby | BSP4 | Y | Y | Y | Y | N | Erlang | Active | Apache | | GoldenOrb | Sponsored | BSP4 | Y | N | N | N | ? | Hadoop 0.20 | Dead? | Apache | | HipG | Academic | MPI | Y | Y6 | N | Y7 | N | Ibis MPJ | None | GPL | | Signal/Collect | Academic | MPI | Y | Y | N? | Y | N/A8 | Proprietary Scala8 | Active | Apache | | Trinity | Academic | MPI | Y | Y6 | N | N? | Y | Proprietary .NET | ? | Not publicly available | | Haloop | Prototype | MapReduce | N | N | N | N | Y9 | Hadoop 0.20 (fork) | Active | Apache |
1. V=vertex object model, A=aggregators, C=message combiners, M=explicit support for topology mutations 2. 0.5.0 is not released yet; the information comes from the 0.4.0 documentation and the source code for 0.5.0-RC2 3. Undergoing transition to Apache Top-Level Project 4. inspired by Pregel 5. the project compiles and the example runs with Hadoop 1.0.2 6. Through operations called “reducers” 7. “On the fly” graphs 8. version 2.0 will be based on Akka 2.0, to enable distribution of the computation 9. Assuming that Hadoop’s native HA capabilities were brought forward into Haloop 10. Hadoop fork
Stricly speaking, none of those solutions have known references in production, and none of them comes with a significant collection of algorithms from the graph theory. Apache Hama and Giraph look more promising because of their open-source nature, their activity and their proven technical foundation – i.e. Hadoop. Between the two Hama is more mature, and more flexible (not purely graph-oriented), but Giraph has contributions from people working at big Internet companies (Yahoo!, Facebook, Twitter, Linkedin) that have always been strong supporters of the open-source ecosystem.
Our next step, at OCTO, will be the implementation of a real use case with (probably) one of the solutions that were presented in this article. This will be the opportunity to look deeper into the products, to challenge their maturity, their robustness and HA capabilities! And of course, if other promising graph processing platforms come to our knowledge, we’ll write about them.
In addition to the project home pages linked in the article, here are some reading suggestions: