L’une des premières choses que l’on apprend en Machine Learning est qu’il faut souvent faire un compromis entre la performance d’un modèle et son interprétabilité. Les modèles transparents (interprétables by design, ou directement interprétables par un humain, comme la régression linéaire ou les arbres de décision) sont en général moins performants que les modèles boîte noire, c.à.d qui ne sont pas directement interprétables par l’humain, comme XGBoost ou les réseaux de neurones artificiels.
Cet article propose une introduction à des méthodes d’interprétation de modèles de Machine Learning qui, on l’espère, vous rendront (ou les utilisateurs de votre modèle) moins frileux vis-à-vis de l’utilisation des modèles boîte noire. Les méthodes citées sont agnostiques au modèle, c’est-à-dire qu’elles peuvent être utilisées sur n’importe quel modèle. Elles sont toutes utilisables pour la régression, ainsi que la classification lorsque l’output du modèle est une probabilité ou un score lié à l’appartenance à une classe.
Certaines sont globales (expliquent le comportement du modèle de façon globale), tandis que d’autres sont locales (expliquent la prédiction d’une seule instance de données).
Note : Dans cet article, lorsqu’on parle de données tabulaires, cela peut s’étendre à du texte en format Bag of words où chaque colonne représente la présence (valeur égale à 1) ou absence (valeur égale à 0) d’un mot dans une instance donnée (phrase, commentaire, etc.)
Données utilisées : Pour les exemples en python, nous avons utilisé:
Tableau-résumé : Voici tout d’abord un tableau résumant l’utilisation potentielle en python des méthodes expliquées dans l’article :
| Méthode | Globale ou Locale | Implémentée dans les librairies citées pour des données | Implémentée dans les librairies citées pour classif/ régression | Requiert les données d’entraînement | ||
| Tabulaires | Images | Texte | ||||
| LIME | Locale | x | x | x | Les 2 | Uniquement tabulaires |
| Feature Permutation | Globale | x | Les 2 | |||
| SHAP | Locale | x | x | Les 2 | Pas TreeSHAP | |
| Exemples contrefactuels | Locale | x | x | Classification | ||
| Ancres | Locale | x | x | x | Classification | Uniquement tabulaires |
On entraîne un modèle transparent sur les prédictions du modèle boite noire à interpréter, au lieu des données labellisées sur lesquelles ce dernier a été entraîné.
On peut donner en entrée les mêmes features que celles du modèle à interpréter, ou si elles ne sont pas compréhensibles par un humain à cause du feature engineering, on peut utiliser les features originales à leur place. On peut aussi sélectionner un sous-ensemble de features du modèle à interpréter au lieu de les utiliser toutes, afin d’alléger l’interprétation.
On utilise ensuite le modèle transparent comme substitut pour interpréter les résultats du modèle boite noire.
Facile à interpréter by design, puisque se base sur des modèles transparents.
Flexibilité quant aux features, modèle et langage utilisés.
Le modèle transparent pourrait donner une bonne estimation du modèle étudié pour une grande partie de notre échantillon de données, mais être très différent pour un sous-ensemble de l’échantillon. On aurait donc une mauvaise interprétation pour ce sous-ensemble.
Requiert l’entraînement d’un modèle.
C’est une implémentation du concept de substitut, pour une instance unique.
On génère un échantillon de données à partir de l’instance qui nous intéresse en :
Cet échantillon est ensuite passé à notre modèle boîte noire pour avoir des prédictions.
Ensuite, un modèle transparent linéaire est entraîné sur ce même échantillon, mais avec un poids pour chaque instance, basé sur la similarité de cette dernière avec l’instance étudiée.
Le poids que ce modèle donne à chaque feature représente l’importance de celle-ci dans l’explication donnée par LIME.
Facile à interpréter by design, puisque se base sur des modèles interprétables.
Flexibilité quant aux features utilisées.
Requiert l’entraînement d’un modèle pour chaque instance à expliquer.
Biais dû à une hypothèse de non-corrélation entre features. En effet, l’échantillon d’entraînement généré ne prend pas en compte les corrélations potentielles entre les features du modèle, ce qui peut donner des combinaisons de valeurs aberrantes, par exemple un appartement de 20m2 composé de 4 pièces.
Les résultats peuvent varier dépendant de l’échantillonnage.
On peut utiliser la librairie lime, et plus particulièrement lime.lime_tabular, lime.lime_image ou lime.lime_text dépendant du type de données.
Il faut savoir que lime.lime_image n’est implémenté que pour les images RGB.
import lime.lime_tabular
explainer = lime.lime_tabular.LimeTabularExplainer(train_boston_X.values, mode='regression',training_labels=train_boston_y,
feature_names=boston_dataset.feature_names, categorical_features=['CHAS'])
explanation = explainer.explain_instance(test_boston_X.values[0], sklearn_regressor.predict)
explanation.show_in_notebook()
N.B : Il faut utiliser predict_proba avec les modèles de classification de scikit-learn.
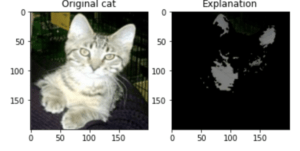
La différence de couleur nous montre tout d’abord les features qui contribuent à augmenter la valeur prédite (en orange) et celles qui au contraire contribuent à la réduire (en bleu).
On voit la valeur exacte de chaque feature de l’instance dans le tableau de droite, mais c’est surtout le graphe du milieu qui nous en apprend le plus sur la contribution de chaque feature à la prédiction. Par exemple, le fait que la valeur de LSTAT (9.04) soit comprise entre 6.77 et 10.93 semble justifier sa contribution positive avec une importance de 1.58
Pour les images :
import lime.lime_image
from skimage.segmentation import mark_boundaries
import matplotlib.pyplot as plt
labels = {0: 'cat', 1: 'dog'}
image_explainer = lime.lime_image.LimeImageExplainer()
explanation = image_explainer.explain_instance(test_rgb_X[0], rgb_estimator.predict, hide_color=0)
temp, mask = explanation.get_image_and_mask(explanation.top_labels[0], positive_only=True, hide_rest=True)
fig, ax = plt.subplots(1, 2)
ax[0].imshow(test_rgb_X[0].astype('int'))
ax[0].set_title(f'Original {labels[test_rgb_y[0]]}')
ax[1].imshow(mark_boundaries(temp / 2 + 0.5, mask).astype('int'))
ax[1].set_title(f'Explanation')
plt.show()
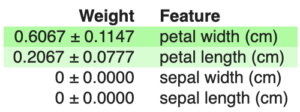
Cette méthode mesure l’impact sur l’erreur de prédiction lorsque les valeurs d’une feature sont permutées.
Pour un ensemble de données labellisées, on calcule tout d’abord l’erreur de notre modèle sur ces données (par exemple en utilisant l’erreur quadratique moyenne). Ensuite, on permute aléatoirement les valeurs de la feature qui nous intéresse (toutes les colonnes de la matrice de données restent inchangées sauf celle de la feature qui nous intéresse), puis on mesure la nouvelle erreur de prédiction. L’importance de la feature est obtenue en calculant la différence ou le ratio entre cette nouvelle erreur et l’erreur originale.
Plus l’erreur de prédiction augmente avec notre permutation, plus la feature est importante.
Simple à interpréter.
Pas besoin d’entraîner un modèle.
Les résultats peuvent varier énormément, car la permutation est aléatoire.
Biais dû à une hypothèse de non-corrélation entre features. En effet, la permutation ne prend pas en compte la corrélation potentielle entre la feature qui nous intéresse et les autres features du modèle, ce qui peut donner des combinaisons de valeurs aberrantes.
On peut utiliser les librairies :
import eli5
fitted_perm = eli5.sklearn.PermutationImportance(sklearn_regressor).fit(test_boston_X, test_boston_y)
eli5.show_weights(fitted_perm, feature_names=boston_X.columns.to_list())
C’est une méthode d’estimation des valeurs de Shapley (théorie des jeux coopératifs), ou plutôt plusieurs méthodes d’estimation, telles KernelSHAP qui est inspirée de LIME (voir 1.2), et TreeSHAP qui est destinée aux modèles basés sur les arbres.
Pour une instance donnée, la valeur de Shapley d’une feature (ou d’un groupe de features) est sa contribution à la différence entre la valeur prédite par le modèle et la moyenne des prédictions de celui-ci
Pour calculer les valeurs de Shapley de features pour une instance, on simule différentes combinaisons de valeurs de features, sachant qu’on peut avoir des combinaisons où une feature est totalement absente. Pour chaque combinaison, on calcule la différence entre la valeur prédite et l’espérance, c.à.d la moyenne des prédictions sur les données réelles.
La valeur de Shapley d’une feature est alors la moyenne de la contribution de sa valeur à travers les différentes combinaisons.
Pour simplifier, supposons que pour une instance donnée du dataset iris, notre modèle prédit la classe "versicolour" avec un score 60% lorsque la largeur des pétales est égale à 1.3cm, leur longueur est égale à 4.5cm, etc. Si en ne changeant que la valeur de la largeur des pétales, en remplaçant 1.3 par 2cm, le score baisse de 10%, alors la contribution de la valeur 1.3cm était de 10%.
Pourquoi a-t-on besoin d’une estimation des valeurs de Shapley ?
En théorie, il faudrait combiner toutes les valeurs que prend chaque feature du modèle dans notre ensemble de données. On se retrouve avec un coût de calcul beaucoup trop élevé.
Base théorique solide
La compréhension des valeurs de Shapley n’est pas très intuitive.
Le temps de calcul reste élevé, surtout pour KernelSHAP.
La librairie alibi implémente KernelSHAP et TreeSHAP (uniquement pour données tabulaires), tandis que la librairie shap implémente plus d’estimateurs, comme le DeepSHAP pour les réseaux de neurones artificiels.
shap s’utilise avec des données tabulaires comme suit:
import shap
explainer = shap.KernelExplainer(sklearn_regressor.predict, train_X)
shap_values = explainer.shap_values(test_X.iloc[0])
N.B : avec un modèle de classification keras il faut utiliser la fonction predict_classes
Cette librairie nous offre plusieurs façons de visualiser les valeurs de Shapley, dont :
shap.waterfall_plot(explainer.expected_value,shap_values,test_X.iloc[0])
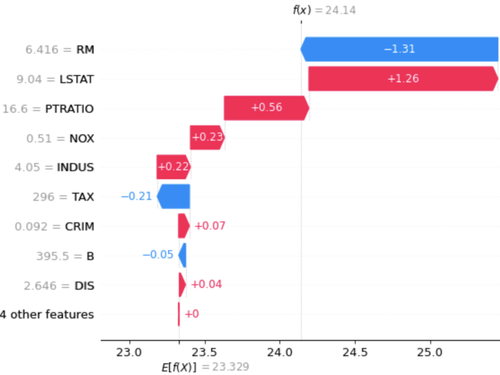
Si on commence la lecture du plot par le bas, on voit que le gain ou la perte par rapport à la moyenne des prédictions est égale à 0, puis en remontant, on a un gain de 0.04 grâce à la valeur 2.646 de la feature DIS, puis une perte de 0.05 à cause de la valeur 395.5 de la feature B, etc. Ainsi, on peut visualiser pour cette coalition de valeurs la contribution de chacune à la différence entre f(x) et E(f(X)).
Pour une image :
explainer = shap.DeepExplainer(digits_estimator, train_X)
shap_values = explainer.shap_values(test_X[0].reshape(1,8,8,1))
shap.image_plot(shap_values, -test_X[0].reshape(1,8,8,1))
Chaque ligne représente une instance. La première colonne est notre vraie image et les autres représentent chacune une classe (0 à 9 de gauche à droite). Pour une colonne donnée, les carrés rouges ont augmenté la probabilité (ou score s’y apparentant) de prédire cette classe, tandis que les carrés bleus l’ont réduite. Par exemple le fait que la partie en haut à droite soit vide élimine le fait que ce soit un 9 (rouge pour la colonne 7, bleu pour 11).
Cette méthode nous montre comment une instance doit changer pour que sa prédiction change.
Il y a plusieurs approches possibles. L’une d’elles consiste pour une instance donnée, à fixer la nouvelle valeur que l’on souhaite être prédite par le modèle, puis de modifier l’instance en essayant de minimiser d’un côté la distance entre l’instance originale et l’instance générée, et de l’autre côté la différence entre la valeur réellement prédite pour l’instance générée et la prédiction souhaitée . L’instance générée est l’explication contrefactuelle.
Pas besoin d’accéder aux données d’entraînement, ce qui peut être important pour des raisons de confidentialité
On n’est pas sûr de trouver un exemple contrefactuel
Implémentation python open-source seulement pour la classification sur des données tabulaires ou des images.
On peut utiliser la librairie alibi comme suit :
from alibi.explainers import CounterFactual
instance = test_digits_X[0].reshape(1, 8, 8, 1)
cf = CounterFactual(digits_estimator, instance.shape)
explanation = cf.explain(instance)
predicted_class = explanation.cf['class']
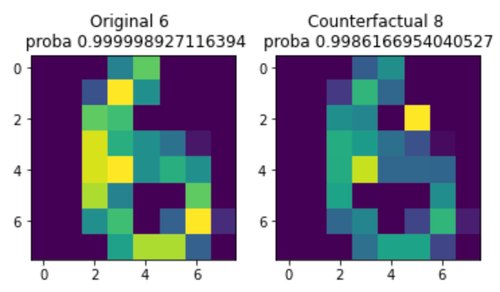
On voit qu’en ajoutant un carré jaune en haut à droite, on forme une boucle, donc notre instance est interprétée comme un 8 au lieu d’un 6.
Cette méthode tente d’expliquer une prédiction sous forme de règle (appelée ancre) de type: IF feature1=valeur1 AND feature2=valeur2 …. THEN PREDICT prédiction.
Pour une instance donnée x, et pour une règle applicable à x (valeur de feature ou combinaison de valeurs de features), on explore le voisinage de x (réel ou généré) à la recherche d’autres instances partageant cette règle. Une règle est une ancre potentielle pour x si le pourcentage des instances respectant cette règle qui ont la même prédiction que x dépasse un certain seuil 𝛕. Ce pourcentage est appelé précision de l’ancre.
Ce processus peut identifier plusieurs ancres, d’où l’intérêt du concept de couverture (coverage), qui représente la probabilité qu’une ancre soit applicable au voisinage de x et donc permet d’expliquer une plus large partie du modèle, et qu’on essaie de maximiser.
Simple à interpréter
Calcul parallélisable
Implémenté en python open-source uniquement pour la classification
On peut utiliser la librairie alibi, notamment la classe AnchorTabular pour les données tabulaires, et AnchorImage pour les images :
from alibi.explainers import AnchorTabular
class_names = list(iris_dataset.target_names)
instance = test_iris_X.iloc[0].to_numpy()
explainer = AnchorTabular(sklearn_classifier.predict_proba,feature_names)
explainer.fit(train_iris_X.to_numpy(), disc_perc=(25, 50, 75))
explanation = explainer.explain(instance, threshold=0.95)
prediction = class_names[explainer.predictor(instance.reshape(1, -1))[0]]
print('Anchor: %s' % (' AND '.join(explanation.anchor)))
print(f'Prediction : {prediction}')
print(f'Precision: {explanation.precision} and coverage : {explanation.coverage}')
Ce qui nous donne une explication très facilement compréhensible car proche du langage humain : 
L'explication du comportement d'un modèle de machine learning, de manière approximative mais surtout facilement compréhensible par un humain, est une étape importante pour son adoption, que ce soit pour des raisons légales (où l'on va privilégier les valeurs de Shapley) ou tout simplement parce que les utilisateurs de notre système intelligent ont besoin de comprendre ce qui se passe à l'intérieur de la boîte noire.
Cet article n’étant qu’une introduction à l’interprétation de modèles, nous vous recommandons vivement de lire “Interpretable Machine Learning” de Christoph Molnar pour creuser une des méthodes introduites ici, ou en découvrir d’autres.