Article co-écrit par Ilann Mahou et Amric Trudel
On nous demande régulièrement chez Octo de développer des outils pour guider la prise de décisions. Par exemple, un client peut chercher à maximiser ses profits, alors qu’un autre souhaite minimiser ses pertes. On cherche souvent à développer des modèles de Machine Learning pour ce type de cas d’usage, mais il faut se rappeler que, bien que ces derniers puissent être excellents pour faire des prédictions, ils ne sont pas conçus pour nous dire comment intervenir dans un système pour l'influencer. Le Machine Learning a simplement pour objet de détecter des corrélations, et l’on a souvent tendance à l’oublier lorsqu’on en tire des interprétations causales de manière hâtive.
Depuis plusieurs années, le domaine de la causalité s’intéresse à ce genre de questions et aborde la modélisation avec une toute autre approche que le Machine Learning. Les concepts de cause et d'effet sont omniprésents dans le raisonnement humain. En effet, nous ne savons pas raisonner autrement que de la manière suivante: « Il s’est passé ceci car ces différentes causes étaient présentes ». Cette conception nous permet ainsi d’agir sur le monde: « Afin de reproduire cet effet, il faut que j’en rassemble les causes ».
L’objectif de cet article est de présenter l’inférence causale, ses apports, son fonctionnement et de fournir aux lecteurs Data Scientists des outils facilitant sa mise en place et son implémentation. Tout du long, nous utiliserons l’exemple d’un gérant de magasin qui cherche à connaître l’impact des promotions qu’il propose sur ses ventes, afin de savoir s'il devrait en proposer plus ou moins.
Le problème principal de la causalité est qu’elle est impossible à observer directement. La seule manière d’observer réellement un lien entre une cause et son effet est de comparer deux situations identiques où seule la cause est altérée. Ainsi, dans notre exemple pour connaître le réel effet des promotions sur les ventes, le seul moyen 100% fiable serait d'utiliser une machine à voyager dans le temps. En observant l’effet des promotions sur une journée précise, il faudrait remonter le temps afin d’observer la même journée avec pour seule différence le fait que l’on ne propose pas de promotions.
Alors dans ce cas seulement, on pourrait affirmer que l’on a réellement observé l’effet causal des promotions sur les ventes au cours de cette journée. Il faudrait alors répéter cette expérience de voyage temporel sur de nombreuses journées différentes pour obtenir un effet causal général (ou moyen).
L’aléatoire comme outil pour étudier la causalité
N’ayant toujours pas inventé le voyage temporel, l’humanité est contrainte pour l’instant de recourir à des astuces pour en simuler l’effet, la plus répandue étant l’aléatoire. C’est ce que l’on fait lors d’essais cliniques contrôlés aléatoires pour évaluer l’effet de nouveaux traitements médicaux. On décide alors au hasard de donner le traitement ou non à chacun des patients participant à l’étude. On le fait aussi dans le monde du développement web avec l’AB testing, où deux versions légèrement différentes d’un site sont proposées et où l’affectation d’un visiteur à la version A ou B du site est décidée de façon aléatoire.
Dans les deux situations, l’ingrédient magique est l’affectation aléatoire à l’une ou l’autre des conditions de traitement. Ainsi, on s’assure que le traitement n’est influencé par aucune autre variable. Lorsque l’expérience est répétée plusieurs fois avec un échantillon suffisamment grand, on peut alors affirmer que la différence mesurée entre le groupe témoin et le groupe expérimental correspond exclusivement à l’effet du traitement.
Il faut noter que ces méthodes de design expérimental, bien qu’omniprésentes en pharmacologie, sont très coûteuses et même souvent impossibles à mettre en place. Le plus souvent, les clients auront collecté des données au fil de l’eau et nous demanderont de les analyser et de les modéliser. On parlera alors de données observationnelles.
Vous devinerez que pour notre gérant de magasin, il n’est pas question de s’amuser à fixer ses promotions de manière aléatoire pendant plusieurs jours pour nous permettre par la suite d’en mesurer l’effet. Il nous faut donc recourir à des méthodes statistiques plus sophistiquées pour travailler avec les données observationnelles qu’il a déjà accumulées et dans lesquelles il n’existe pas de groupe témoin ni de groupe expérimental.
C’est l’objectif de l’inférence causale de permettre l’utilisation d’un historique où l’ensemble des journées avec ou sans promotions ne sont pas directement comparables a priori, car l’attribution des promotions peut avoir été favorisée ou défavorisée par d’autres facteurs. Ainsi, nous chercherons à estimer l’effet causal des promotions entre des journées jugées semblables, toutes choses étant égales par ailleurs. Pour ce faire, il devient important d’identifier toute une série de variables associées au problème observé, qui pourront être mesurées et servir dans l’inférence causale.
La méthodologie l’inférence causale, telle que décrite par les créateurs de la librairie Do-Why, se fait en quatre étapes :
Afin de pouvoir guider la prise de décision de notre client, il est nécessaire de faire la liste de tous les facteurs mesurables qui peuvent influencer les promotions et les ventes. Ce seront nos variables. Une fois cette liste de variables obtenue, il faut saisir les interactions entre elles dans le but de créer un graphe, qui sera notre modèle causal.
Afin de faciliter la mise en place de ce modèle, ainsi que le choix des variables, nous proposons un canevas à remplir avec les clients ou personnes possédant les connaissances métiers nécessaires. Ce canevas commence avec la définition du problème et sa reformulation en question causale. Le problème décisionnel auquel nous faisons face est :
« Les promotions de mon magasin augmentent-elles le chiffre d’affaires ?
Dois-je continuer à les proposer ? »
Afin de le traduire en problème causal, on cherche à faire ressortir deux variables d'intérêt, à savoir :
Le traitement : variable sur laquelle on doit guider la prise de décision, donc elle doit être modifiable par le client.
→ les promotions
La cible : variable de résultat, sur laquelle on cherche à mesurer l’effet du traitement.
→ les ventes


De plus, on cherche à reformuler le problème pour en extraire la question qui y répond simplement de la façon la plus formelle possible. Par exemple, la question _« Les promotions de mon magasin augmentent-elles le chiffre d’affaires ? » p_eut être formalisée en :
« Quel est l’effet moyen des promotions sur les ventes du magasin ? »
Et la question « Dois-je continuer à les proposer ? Ou même en faire plus ? » peut se traduire par un exemple plus précis tel que :
« La semaine dernière nous n’avons pas fait de promotions, qu'auraient été les ventes si on les avait mises en place ? »
Ceci étant fait, il est maintenant nécessaire de définir toutes les variables pouvant avoir un effet, car il pourrait s’agir de facteurs de biais nécessaires à contrôler.
Dans notre cas, nous n’en identifierons trois pour faciliter la compréhension de l’exemple :
Le jour de la semaine (lundi, mardi….)
L’ouverture du magasin (ouvert, fermé)
L’affluence en clients (nombre)



Les effets de toutes ces variables les unes sur les autres peuvent rapidement former un réseau complexe de liens de causalité. Il est alors pratique de les détailler une à une pour enfin tout représenter sous forme de graphe.
Une fois toutes les variables définies et les liens posés, on obtient un graphe qui va servir à la fois d’appui à la réflexion, mais aussi à définir les différentes formules de calcul de l’effet causal.
Dans le cadre de notre exemple, on peut obtenir un graphe tel que celui présenté dans le bas du Canevas.
Trouver les liens de causalité
Dans certains cas, il arrive que l’on ignore le sens de l’effet entre certaines variables ou même si une variable possède ou non un effet sur le modèle. Pour ce genre de cas, une méthode d’exploration nommée Causal Discovery permet de définir les liens et les orientations semblant les plus probables au vu des données. Cette pratique est nécessaire si certains doutes subsistent ou que les connaissances métiers ne sont pas suffisantes pour exprimer la totalité des liens. Ainsi cette méthode de découverte causale vous permettra d’établir les liens principaux et leur sens.
Vous aurez deviné qu’il ne suffit pas, pour estimer l’effet des promotions sur les ventes, de simplement comparer les jours où il y a des promotions avec les jours où il n’y en a pas. On peut facilement calculer la moyenne des ventes pour chaque condition, mais comme expliqué précédemment, il serait naïf de le faire car elles ne sont pas comparables. Pour y parvenir, il faut se ramener au graphe qui a été créé à l’étape précédente. On porte attention aux variables qui influencent à la fois notre traitement et notre cible.
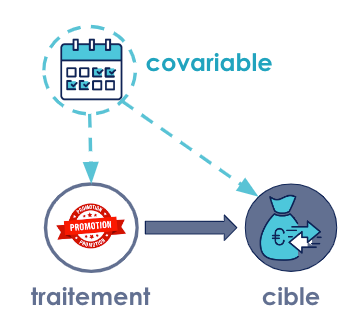
Prenons ici l’exemple du jour de la semaine. On peut imaginer que le gérant ait davantage tendance à proposer des promotions le samedi. De même, il est possible que les clients d’eux-mêmes soient plus enclins à dépenser quand ils viennent le samedi. Dans cette situation, il serait exagéré d’attribuer la hausse totale des ventes à la promotion, car il est possible qu’une bonne partie soit simplement attribuable au fait qu’on soit samedi.
Le jour de la semaine est donc ce qu’on appelle une co-variable (ou confounder en anglais), et il est nécessaire de la contrôler pour obtenir une estimation juste de l’effet causal entre les promotions et les ventes. Il arrive d’ailleurs souvent que l’on ait plusieurs co-variables, et l’inférence causale nous propose un système pour retracer tous les liens et identifier facilement les variables qui doivent être contrôlées. On procède alors à un ajustement des calculs de probabilités, et pour cela il existe plusieurs méthodes.
Reprenons notre exemple précédent, et ajoutons-y une deuxième co-variable : le fait que le magasin soit ouvert ou non. La formule d’ajustement nous sera donnée par un critère qu’on appelle le back-door, qui nous indique de contrôler les valeurs des deux co-variables.
Contrôler les co-variables correspond, sur le graphe causal, à sectionner les liaisons qu’elles ont avec le traitement. On se rappelle qu’une des manières d’y parvenir aurait été de mettre en place un essai contrôlé aléatoire. Ici, comme nous sommes contraints d’utiliser des données observationnelles, nous devons trouver une formule d’ajustement qui permettrait de calculer l’effet causal recherché entre des jours où les co-variables ont des valeurs semblables.
Pour ce faire, nous allons utiliser un opérateur du calcul causal appelé do, introduit par Judea Pearl. Cet opérateur nous permet de représenter l’ajustement de probabilités nécessaire pour agir sur le système causal en fixant nous-même la valeur de la variable promotion. Nous verrons dans la section suivante comment on peut faire ce calcul.
Une fois l’ajustement effectué avec do, nous pouvons calculer des moyennes comparables pour les jours avec ou sans promotion. Avec une simple soustraction, on obtient l’effet global des promotions sur les ventes, appelé effet causal moyen (Average causal effect / ACE).
L’opérateur do permet de simuler la situation où le manager choisirait, pour une même situation, de proposer ou non une promotion, indépendamment de l’influence des covariables.
Les cas d’usage réels comportent en général un grand nombre de variables et un graphe plus complexe. La question qui se pose rapidement est quelles variables doivent être contrôlées, ou non ? Le do calculus développé par Pearl propose tout un système de règles permettant de trouver facilement, à partir du modèle causal graphique, l’ensemble des variables qui doivent être contrôlées, afin de construire la formule pour estimer l’effet causal. Les librairies comme DoWhy permettent de le faire sans effort. La formule obtenue est appelée estimande, et on l’utilisera dans l’étape suivante pour estimer l’effet causal à partir du jeu de données.
Il faut maintenant calculer une estimation statistique de l’effet des promotions sur les ventes à partir des données historiques dont on dispose. Comme on l’a vu, l'échantillon des jours où il y a eu des promotions doit être remanié pour lui retirer les biais correspondant aux influences des co-variables. Pour ce faire, l’inférence causale propose différentes méthodes possibles, selon les types de données dont on dispose, avec des rapidités d’exécution et des niveaux de précision différents. (Voir l’arbre de décision en annexe)
La méthode que nous allons utiliser ici est la pondération par score de propension (propensity score / PS). Cela nous permet d’utiliser dans l’analyse tous les jours renseignés dans le jeu de données, mais en pondérant chaque journée selon la probabilité qu’il y ait eu une promotion, étant donné la situation décrite par les co-variables. Cette probabilité correspond au propensity score. Dans notre cas, il suffit de calculer la proportion de jours avec promotion parmi les effectifs (nombre de jours distincts dans le jeu de données) pour chaque combinaison possible des co-variables.
Dans le tableau suivant, vous pouvez voir que pour chaque ensemble de co-variables (combinaison jour et ouverture) un propensity score différent est calculé.
Cette mesure va nous permettre d’équilibrer le poids de chaque exemple dans le jeu de données. En effet, l’idée dans la pondération via le propensity score est de venir appliquer un poids sur chaque montant de vente en fonction de la probabilité qu’il y ait eu une promotion.
De façon plus précise, on divise les ventes par le propensity score pour les exemples ayant reçu une promotion, et par (1 - propensity score) pour les exemples sans promotion.
Prenons par exemple le premier ensemble de co-variables (Bleu : Lundi - ouvert), la fréquence de cet ensemble est beaucoup plus importante dans le groupe des promotions que dans celui sans promotions (80% contre 20% soit quatre fois plus). Ainsi, les ventes de toutes les occurrences de cet ensemble de co-variables ayant reçus les promotions seront multipliées par 1,25 et par 5 pour le groupe sans promotion.
Pour résumer, pour cet ensemble de co-variables le groupe sans promotion étant 4 fois moins important, il sera multiplié par un facteur 4 fois plus important que celui avec promotion.
Cette méthode nous permet d’égaliser la proportion de chaque ensemble de co-variables entre les deux sous-groupes de traitement (promotions). Autrement dit, elle simule un jeu de données où chaque ensemble de co-variables se trouve de façon égale dans le groupe avec et sans promotion.
Une fois que cela est fait, on peut alors calculer l’effet causal moyen avec les ventes ajustées.
Via cette double approche, l’effet de groupe nous permet d’approcher le cadre théorique de comparer des journées similaires où seules les promotions changent, et donc d’extraire un effet causal le plus réel possible.
Nous avons construit un modèle causal qui peut fournir des estimations. Cependant, il est possible qu’il soit biaisé ou que les hypothèses sur lesquelles il est construit soient fausses. Le but de cette quatrième étape est de venir tester la robustesse du modèle via différentes méthodes de réfutation.
Un risque classique et majeur est d'avoir oublié de mesurer une co-variable exerçant un effet important sur nos variables d'intérêt. Dans notre cas, on pourrait avoir oublié de tenir compte des jours de vacances, qui auraient un effet potentiellement fort sur les promotions ainsi que les ventes. Pour vérifier la probabilité qu’il manque une co-variable importante à notre modèle, nous pouvons utiliser la méthode dite de co-variable aléatoire. Cette méthode de réfutation consiste à générer et à ajouter aux données une variable aléatoire corrélée avec les promotions et les ventes. On calcule alors à nouveau le même effet causal que précédemment, mais dans un modèle qui inclut la nouvelle variable. En répétant cette action avec de multiples variables aléatoires, on vient interroger notre modèle sur la possibilité qu'une co-variable fut oubliée de l’analyse. Ainsi, si l’on a généré une variable aléatoire ayant une distribution proche de celle des vacances, on observerait un changement significatif de l’effet causal précédemment calculé.
Quel que soit le domaine d'intérêt, il est impossible de connaître et mesurer la totalité des facteurs pouvant avoir un effet sur le phénomène d’intérêt. Il ne s’agit d'ailleurs pas d’une utopie ou nécessité. Devoir mesurer un très grand nombre de variables et calculer un modèle qui en découle pourrait augmenter drastiquement le coût en temps et argent, sans garantir une augmentation de la précision.
Ainsi, l’objectif des méthodes de réfutations est de venir confirmer notre sélection de variables comme étant suffisantes pour l’analyse.
Dans le cadre d’études observationnelles, il peut fréquemment arriver qu'on possède un échantillon de données biaisé ou insuffisant. Bien que l’étude causale cherche à contourner ces biais, le doute subsiste. Une approche de réfutation pouvant confirmer la significativité de l’effet trouvé est celle du placebo. Il s’agit d’une méthode relativement simple qui consiste à modifier les données en attribuant aléatoirement les promotions, puis à relancer toute l’analyse causale.
Dans notre première analyse, nous avons trouvé un effet causal moyen de 500€, or si après la permutation on retrouve un effet proche au précédent, on peut alors affirmer qu’il y a un problème (possiblement dans l’échantillon, les variables choisies …). A contrario, si le nouvel effet obtenu est proche de 0, alors il semblerait que l'effet des promotions sur les ventes soit relativement fiable.
Bien que ces méthodes soient pratiques, elles ne permettent pas d’affirmer hors de tout doute que l’effet causal trouvé est exact, elles limitent seulement le risque que notre modèle soit biaisé. Il est donc important de faire un sérieux travail préalable d’identification des variables pertinentes et des liens de causalité avant de se lancer dans une inférence.
L’inférence causale en est encore dans ses premiers balbutiements, mais elle s’annonce très prometteuse. Bien qu’étant majoritairement utilisée dans le milieu médical de nos jours, ses domaines d’applications potentiels sont aussi divers que nos besoins d’aide à la décision. Néanmoins, il reste qu’estimer avec certitude un effet causal n’est pas chose aisée et un des prérequis est qu’il faut posséder un haut niveau de connaissances métier. C’est principalement ce point qui rend son utilisation difficile, si l’on compare avec l’apprentissage supervisé en Machine Learning, ce dernier étant devenu très populaire en raison de ses prédictions de haute précision sans nécessiter d’informations sur l’origine des données.
De plus, comme les connaissances métiers sont encodées dans les modèles causaux sous formes d’hypothèses de départ (ex: “Le jour de la semaine influence l’affluence”), un changement parmi celles-ci risque de considérablement affecter l’estimation de l’effet causal. C’est une réalité à garder en tête, mais nous avons vu qu’il existe tout de même quelques méthodes de réfutation pour vérifier l’adéquation du modèle avec les données. Il sera intéressant de surveiller au cours des prochaines années le développement des nombreuses librairies et outils qui rendront l’inférence causale de plus en plus accessible et pratique. Dans la section annexe vous pouvez trouver les principales librairies et outils existants (majoritairement en python), ainsi qu’un récapitulatif des différentes méthodologies relatives au format des données.
Il existe une multitude de méthodes et d’approches d’inférence causale (et par extension, de librairies). Le choix de l’une ou de l’autre est conditionné par le format des données et le problème à résoudre. Dans un premier temps, nous recommandons de remplir le canevas présenté précédemment dans l’article. Il permettra de réduire le champ des possibles et de clarifier les objectifs, puis d’identifier précisément les variables d’intérêt et leurs types. Dans un second temps, vous pouvez utiliser l’arbre de décision suivant afin de choisir la méthode la plus appropriée et la librairie correspondante. Vous trouverez dans ce repository GitHub un exemple d'utilisation de la librairie DoWhy.
An Introduction to Causal Inference - Judea Pearl.epub, n.d.
Causal Inference in Statistics - Judea Pearl.epub, n.d.
Nogueira, A.R., Pugnana, A., Ruggieri, S., Pedreschi, D., Gama, J., 2022. Methods and tools for causal discovery and causal inference. WIREs Data Min. Knowl. Discov. 12. https://doi.org/10.1002/widm.1449
Shanmugam, R., 2018. Elements of causal inference: foundations and learning algorithms. J. Stat. Comput. Simul. 88, 3248–3248. https://doi.org/10.1080/00949655.2018.1505197
Runge, J., 2018. Conditional independence testing based on a nearest-neighbor estimator of conditional mutual information, in: Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics. PMLR, pp. 938–947.
Sharma, A., Kiciman, E., 2020. DoWhy: An End-to-End Library for Causal Inference. https://doi.org/10.48550/arXiv.2011.04216