J'ai eu la chance d'effectuer, assisté par Alexis Flaurimont, une présentation sur l'utilité de la programmation parallèle lors de Breizh C@mp il y a quelques mois. L'objectif était entre autres de démontrer que la programmation parallèle est de nos jours beaucoup plus accessible qu'il y a quelques années.
Lors de cette présentation, nous avions utilisé la méthode de Monte-Carlo. Il s'agit d'un algorithme fortement parallélisable (les Anglais disent "embarrassingly parallel"). Parfait pour démontrer l'intérêt d'une parallélisation pour augmenter sensiblement les performances d'une application. Je suis même prêt à confesser que l'exemple est même un peu trop idyllique, mais là n'est pas le sujet de cet article. La méthode de Monte-Carlo est habituellement expliquée en calculant la variable Pi. Il s'agit d'une méthode permettant de calculer de façon statistique ce que nous n'arrivons pas à calculer de façon mathématique. Pi est d'ailleurs un mauvais exemple puisqu'il est plus efficace de calculer sa valeur par série. Je vous laisse consulter l'article de Wikipedia, mais l'idée est de faire plusieurs tirages aléatoires et d'en tirer une conclusion.La moyenne de ces conclusions nous donne une approximation du résultat réel. Plus il y a de tirage, plus on s'approche du résultat.
De notre côté, on s'est dit que Pi, c'est un peu surfait et ça ne fait pas rêver. Je me suis donc mis en tête de calculer l'aire du signal de Batman en remplacement. Nettement plus divertissant. Je me suis basé sur une équation ayant fait le tour du Net il y a environ un an. La voici:
Plein de minutie et aidé par Wolfram Alpha, j'ai donc recodé l'équation en Java. À noter que l'équation de Wolfram Alpha est fausse. J'ai cherché comment l'indiquer à Wolfram Alpha mais sans succès. Si quelqu'un connaît la procédure, merci de me l'indiquer en commentaire. Voici la correction. 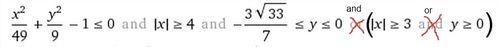
Il y a aussi une version calculant Pi, mais évidemment, comme c'est un rond, ça a tout de suite moins de gueule. Mais c'est pratique pour tester l'implémentation. Revenons à Batman. Le visuel c'est bien joli, mais c'est surtout pour mettre un peu d'entrain dans une conférence. Nous ce qu'on veut, c'est comparer les performances. Pour cela, nous lançons une exécution de 30 secondes. Il s'agit de faire le plus de tirages possibles. Il y a trois implémentations:
Pour vous donner une idée du code, l'implémentation en séquentielle est la suivante:
MonteCarloCalculator calculator = instantiateAlgorithm(constructor, 0);
new MonteCarloCmd(calculator).run();
C'est logique. On appelle le calculateur qui fera la boucle. En parallèle c'est un peu plus compliqué, mais pas beaucoup:
ForkJoinPool pool = new ForkJoinPool(); // creation du pool
for (int i = 0; i < pool.getParallelism(); i++) {
MonteCarloCalculator calculator = instantiateAlgorithm(constructor, i); // un calculator par processeur
pool.execute(new MonteCarloCmd(calculator)); // on lance l'exécution de se calculator en parallèle sur le pool }
try {
latch.await(TIMEOUT, TimeUnit.SECONDS); // Le pool attend que toutes les tâches soient terminées
} catch (InterruptedException e) {
throw new RuntimeException(e);
}
pool.shutdown(); // fermeture du pool (qui aurait pu être réutilisé au besoin)
Le vrai code disponible sur GitHub est un peu plus complexe, car j'ai mis en place un pattern listener pour avoir l'évolution des résultats au fil de l'eau. Cette implémentation est d'ailleurs pénalisante pour la version parallèle. L'algorithme classique du Monte-Carlo en parallèle est de faire les tirages dans des threads séparés. Ceux-ci présentent des résultats partiels au contrôleur qui se charge de calculer le résultat final. Dans le cas présent, pour pouvoir fournir des résultats provisoires au fil de l'exécution, une référence atomique est utilisée pour agréger les résultats. Il y a donc une contention sur cette variable. Ce qui ne serait pas le cas pour une implémentation plus classique. Pour les curieux, l'équation ci-haut en version Java est la suivante:
// Wings bottom
if (pow(x, 2.0) / 49.0 + pow(y, 2.0) / 9.0 - 1.0 = 4.0 && -(3.0 * sqrt(33.0)) / 7.0 = 3.0 && -(3.0 * sqrt(33.0)) / 7.0 = 0) {
return true;
}
// Tail
if (-3.0 = 0 && 3.0 / 4.0 = 0) {
return true;
}
// Ears inside
if (1.0 / 2.0 = 0 && y >= 0) {
return true;
}
// Chest
if (abs(x) = 0 && 9.0 / 4.0 - y >= 0) {
return true;
}
// Shoulders
if (abs(x) >= 1.0 && y >= 0 && -(abs(x)) / 2.0 - 3.0 / 7.0 * sqrt(10.0) * sqrt(4.0 - pow(abs(x) - 1.0, 2.0)) - y + (6.0 * sqrt(10.0)) / 7.0 + 3.0 / 2.0 >= 0) {
return true;
}
return false;
Des tests ont été effectués sur un Cluster GPU Quadruple Extra Large chez Amazon. Nous avons donc 16 coeurs CPU et 996 coeurs GPU. Voici les résultats pour 30 secondes d'exécution:
En parallèle, nous avons un gain notable, mais pas autant que l'on aurait pu espérer. On peut sûrement faire mieux, car, comme je vous disais, l'implémentation est désavantageuse pour le parallèle. Ce qui n'est pas plus mal. Il s'agit d'une belle démonstration de la loi d'Amdahl.
Une chose à retenir: Pendant que la version séquentielle n'utilise qu'un seul CPU, la version parallèle utilise tous les CPUs à sa disposition. Ceci en restant simple d'implémentation.
Pour la version GPU, l'impression de simplicité est plus mitigée. La bonne nouvelle c'est qu'Aparapi est assez bluffant. Il s'agit d'une librairie Java traduisant le bytecode du kernel (nom donné à un programme s'exécutant sur GPU) de votre application en une implémentation OpenCL. Le tout est ensuite appelé via du JNI. C'est développé par AMD. On arrive à y faire tourner une multiplication de matrice en 10 minutes. La mauvaise nouvelle c'est que pour un Monte-Carlo, c'est un peu plus compliqué. Voici, en vrac, quelques problèmes que vous pourriez rencontrer.
java.util.Random ne fonctionne pasDe plus, vous n'obtiendrez malheureusement pas d'aussi hautes performances avec Aparapi que si vous codiez en CUDA. Mais tranquillement, l'écart se resserre. Il y a par exemple de nouvelles options de gestion mémoire. La localisation de la donnée est très importante en GPU. Reste que, vous avez sûrement remarqué, sans forcer sur l'optimisation, la version GPU est 17 fois plus rapide que la version parallèle!
Ma conclusion est donc la suivante:
Et en attendant, let Batman rise.