Dans un article précédent, nous avons expliqué notre approche pour appliquer l’apprentissage par renforcement (RL - Reinforcement Learning) à la conduite autonome dans un simulateur. Nous avons explicité les concepts du RL dans ce cas d’usage et décrit l’algorithme de DDQN (Double Deep-Q Learning) que nous avons choisi pour ce problème. Si vous n’avez pas lu l’article précédent, retenez simplement que :
Rappelez-vous de la conclusion de notre article précédent : “tout ce qu’est capable de faire un algorithme de RL est de maximiser un signal de récompense”. Vous l’aurez compris, le choix de la récompense est crucial et c’est ce que nous allons expliciter dans un premier temps.
On veut que la fonction de récompense indique à l’agent si les actions qu’il entreprendra dans l’environnement vont l’amener à conduire de façon autonome. Dans un problème de conduite autonome, on peut imaginer toutes sortes de fonctions de récompense en fonction des informations que nous fournit la simulation. Ces informations peuvent concerner par exemple :
Vous l’aurez compris, c’est un choix assez subjectif qui dépend de ce que l’on entend par “conduire de façon autonome”. Nous nous en tiendrons ici à deux fonctions de récompense mentionnées dans l’approche de Felix Yu. Toutes deux utilisent la distance au centre de la route, ou CTE (Cross Track Error) pour les intimes.
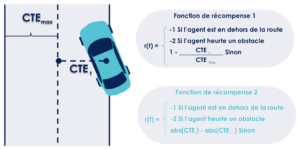
La première fonction de récompense que nous allons étudier consiste à récompenser l’agent de façon absolue par rapport à la CTE. La récompense est maximale (elle vaut 1) lorsque la CTE est nulle et que la voiture est au centre de la route. Elle est minimale (elle vaut 0) lorsque la CTE est maximale et que la voiture est au bord de la route. Dans ce premier cas de figure, pour que l’agent réussisse à maximiser sa récompense, il doit logiquement se tenir proche du centre de la route.
La deuxième fonction de récompense consiste à récompenser l’agent de façon relative en se basant sur la différence entre la CTE à un instant t et la CTE à un instant t+1. Dans ce deuxième cas de figure, l’agent doit se rapprocher du centre de la route pour maximiser sa récompense, peu importe qu’il en soit déjà proche ou non.
Nous allons étudier les impacts de cette différence sur notre agent et sur ses performances. Les deux fonctions de récompense doivent en théorie amener l’agent à atteindre son but, qu’en est-il en pratique ?
Prenons un peu de temps pour mesurer l’ampleur de la tâche qui nous attend. Nous n’avons a priori aucune idée du temps nécessaire pour que notre algorithme converge, celui-ci peut prendre des heures, des jours, voire plus. Celui-ci peut aussi ne pas converger, car souvenez-vous que la convergence de l’algorithme que nous utilisons n’est pas garantie dès que l’on utilise des réseaux de neurones. De plus, les paramètres de notre algorithme, que nous avons volontairement omis de vous préciser jusqu’à maintenant, sont nombreux : taille et architecture du réseau de neurones, pré-traitement appliqué à l’image, etc. Il en est de même pour le simulateur : couleur et texture de la route, tracé du circuit etc.
Choisir tous les paramètres d’un problème d’apprentissage automatique constitue à elle seule une discipline que l’on appelle l’ingénierie des caractéristiques (ou feature engineering). Dans la pratique, entraîner un algorithme de RL pour un problème aussi complexe que celui de la conduite autonome est un long périple dans lequel il est facile de se perdre.
Commençons par définir clairement notre objectif et les métriques associées. Cela nous permettra de mesurer une amélioration ou une régression entre deux expériences et d’en tirer des conclusions sur le choix des paramètres de notre agent et du simulateur. Il s’agit de répondre aux questions suivantes :
Comment mesure-t-on si un agent conduit de façon autonome ? Comment dire si un agent entraîné est meilleur qu’un autre ?
Lorsque nous allons entraîner notre agent, comment savoir si et quand on considère qu’il a terminé son entraînement ?
Nous avons choisi de mesurer la capacité à conduire de façon autonome en mesurant la distance parcourue dans le simulateur sans sortir de la route. Ainsi, entre deux agents entraînés, l’un sera considéré comme meilleur s’il parcourt une distance d1 supérieur à une distance d2 obtenue par un autre agent peu importe comment l’agent conduit: qu’il fasse des zigzags ou prenne la corde dans les virages.
Nous mesurons les métriques suivantes pendant l’entraînement de notre agent :
Définir ces mesures nous permet de garder un cap et de tirer des conclusions concernant nos différents paramètres. Dans la pratique, nous avons mis plusieurs mois avant d’obtenir un agent dont on peut dire qu’il conduit de façon autonome lorsqu’on l’observe dans le simulateur. Les déceptions ont été nombreuses, ce cadre d’expérience nous garantit aussi que l’on ne se décourage pas en chemin.
Tip 1 : Ne vous précipitez pas et ne vous attendez pas à avoir d’emblée des modèles qui convergent.
Entre la simulation et votre modèle, il y a probablement beaucoup de paramètres pour lesquels vous n’aurez pas d’emblée une idée précise. Pour certains, il peut être difficile de s’en faire une idée autrement que par l’expérience. Allez-y progressivement, l’essentiel est que vous partiez de quelque part. Peu importe si les résultats vous paraissent “bons” ou “mauvais” : vos métriques vous fourniront une mesure objective de vos résultats.
Prenez également le temps de mettre en forme vos métriques. Organisez les résultats que vous obtenez, par exemple sous la forme d’un carnet d’expériences. Ne vous découragez pas et prenez régulièrement du recul pour observer le chemin parcouru et identifier les décisions qui vous font avancer dans la bonne direction. Cela vous permettra également d’en faire profiter les autres (par exemple en mettant un commentaire sous cet article ;)).
Nous ne ferons pas ici une liste exhaustive de toutes les expériences que nous avons menées et de tous les paramètres que nous avons testés. Nous vous proposons par contre de nous attarder sur le résultat de quelques expériences qui ont fonctionné et nous vous exposerons par la suite les conclusions que nous en avons tirées concernant les paramètres du modèle et de la simulation.
Nous avons entraîné un agent avec la première fonction de récompense pour un indice d’exploration de 10 000.
Un mot sur l’indice d’exploration
Le dilemme Exploration VS Exploitation est une question centrale en apprentissage par renforcement. Faut-il exploiter sa connaissance en maximisant ses chances de récompense future ? Autrement dit, faut-il capitaliser sur ce que l’on pense déjà connaître ?
A l’inverse, faut-il explorer de nouvelles possibilités pour accumuler une expérience variée et donc plus juste ?
La réponse à cette question n’est pas évidente, et l'algorithme utilisé est régi par un paramètre nommé indice d'exploration pour répondre à ce dilemme. Rappelez-vous de notre premier article, l’agent utilise une politique “epsilon-greedy” lors de son entraînement. Ainsi sur une étape d’apprentissage, après avoir interrogé son réseau de neurones pour savoir quelle action est la meilleure compte-tenu de sa connaissance actuelle il peut choisir :
Notre algorithme de DDQL commence avec une valeur d’epsilon à 1 (toutes les actions prises sont aléatoires) et décroit progressivement sa valeur jusqu’à une valeur faible, typiquement 0,1. L’indice d’exploration va décrire le nombre d’étapes sur lequel on choisit de faire décroître le paramètre epsilon de 1 à 0,1. Ainsi, l’agent explore fortement en début d’entraînement lorsqu’il est peu expérimenté, et fait au fur et à mesure de plus en plus confiance à ses prédictions en exploitant sa connaissance.
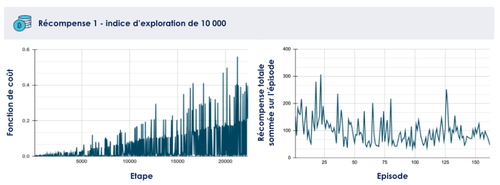
Après un entraînement de l’agent sur 20 000 étapes, nous constatons que la fonction de coût du réseau de neurones augmente en tendance (cf figure 2), indiquant que le modèle ne converge pas. L’évolution de la récompense sommée sur l’épisode montre également que l’agent ne semble pas réussir à maximiser la récompense.
Tip 2 : Ne vous acharnez pas à entraîner indéfiniment un agent qui ne converge pas. Nous avons observé dans l’état de l’art que l’entraînement de tels modèles se faisait en général sur un nombre d’étape supérieur à l’indice d’exploration, mais jamais significativement plus grand en termes d’ordre de grandeur. C’est ce que nous avons constaté également expérimentalement, un agent qui a réussi à apprendre avec un indice d’exploration de N va commencer à converger quelque part entre N et quelques fois N (très grossièrement) étapes dans l’environnement.
Une explication de ce phénomène est notamment que l’agent apprend peu après N étapes dans l’environnement. A partir de ce moment, son paramètre epsilon est fixé à une valeur faible: l’agent fait donc confiance à son réseau de neurones (son oracle) pour prendre des décisions.
En pratique, nous avons constaté que l’agent avait tout de même besoin de confronter sa politique à la réalité pour affiner ses prédictions, convergeant souvent après N étapes. Il est donc souhaitable de que l’entraînement dépasse N étapes, mais si un agent n’a montré aucun signe de convergence après 4 ou 5 fois N étapes dans l’environnement, rien ne sert de s’acharner. Augmentez éventuellement l’indice d’exploration en lançant un nouvel entraînement ou bien cherchez le problème ailleurs : fonction de récompense, modèle, réseau de neurones etc.
Il n’est pas utile d’entraîner ce modèle plus longtemps, le nombre d’étapes d’entraînement a déjà largement dépassé l’indice d’exploration et l’agent n’explore plus.
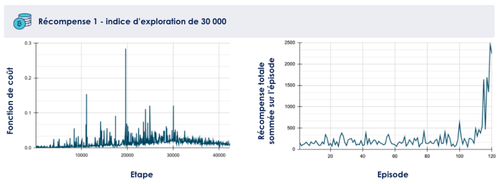
Lorsqu'on entraîne ce même modèle avec un indice d’exploration plus élevé (de 30 000) sur environ 40 000 étapes, on observe cette fois-ci que la fonction de coût finit par diminuer (cf figure 3), indiquant que le réseau de neurones a convergé vers un état où ses prédictions sont proches des valeurs attendues (selon l’indication qui lui est fournie par la fonction de récompense). La récompense finit également par augmenter, et l’agent réalise en fin d’entraînement quelques épisodes particulièrement au-dessus du lot.
Tip 3 : Identifier les ordres de grandeur concernant le nombre d’étapes dans l’environnement et l’indice d’exploration pour votre cas d’usage est crucial.
Ils déterminent le temps d’entraînement et donc le coût de vos modèles. Utilisez la littérature scientifique en y trouvant des cas d'usages similaires aux vôtres. Cherchez notamment des expériences qui ont des espaces des états et des espaces des actions de tailles similaires aux vôtres. Ces expériences vous donneront une estimation très grossière (est-ce qu’on est plutôt sur 10 000 ou 1 000 000 étapes dans l’environnement ?). Explorez ensuite autour de ces valeurs pour identifier des modèles qui montrent des signes de convergence (cf. fonction de coût du réseau de neurones par exemple).
Gardez en tête que les principaux paramètres qui vont déterminer votre nombre d’étape et votre indice d’exploration sont :
- La taille de l’espace des états - le nombre d’états différents que votre agent peut potentiellement rencontrer. Dans notre cas d’usage, l’état est représenté par une image de la route vue par la caméra frontale de la voiture. Plus l’espace des états est grand, plus le nombre d’étapes dans l’environnement (et donc l’indice d’exploration cf. Tip 1) est grand, car votre agent à un spectre plus large à explorer et va probablement mettre plus de temps à converger.
- La taille de l’espace des actions - le nombre d’actions différentes que peut entreprendre votre agent à chaque étape dans l’environnement. Dans notre cas d’usage il est de 5 (cf Article 1). Plus l’espace des actions est grand, plus le nombre d’étapes dans l’environnement doit être grand car les possibilités augmentent pour l’agent qui a besoin de plus de temps pour apprendre l’influence de ces différentes actions dans l’accomplissement de son objectif.
- La fonction de récompense. Difficile de décrire un lien évident entre ce paramètre et le nombre d’étapes nécessaires à la convergence. Cela dépend de chaque cas d’usage, mais vous pourrez vous forger progressivement une intuition de l’influence de ce paramètre pour votre cas d’usage.
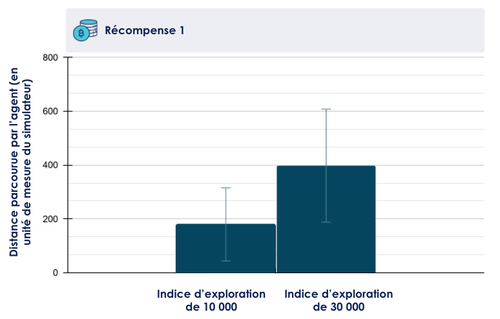
L’évaluation de ces agents montre des performances intéressantes. Avec un indice d’exploration de 30 000 notamment, la voiture parcourt en moyenne une distance 400 (en unité de distance dans le simulateur), soit le double par rapport à un indice d’exploration de 10 000 (cf figure 4). Cela correspond par observation au passage de quelques courbes dans le circuit. L’écart-type est en revanche très important, quasiment 100% de la valeur moyenne. En effet, l’observation montre que l’agent se vautre parfois lamentablement et sort de la route avant d’avoir franchi le premier virage. Cela indique notamment que la politique trouvée par l’agent est loin d’être optimale. Le réseau de neurones a convergé, mais vers un état où il ne sait toujours pas prédire correctement l’issue de certaines situations (il tourne encore à droite dans certains virages à gauche et inversement par exemple).
Tip 4 : N’oubliez pas d’évaluer vos agents en situation et ne vous fiez pas seulement à vos métriques.
On a souvent pour réflexe de regarder en premier lieu nos graphiques. Oubliez vos réflexes d’apprentissage supervisé, où le problème est souvent mieux cadré et la réponse que vous voulez obtenir est claire (puisque vos données sont labellisées). Ne vous attendez pas à obtenir de belles courbes avec une tendance facile à observer. Analysez bien toutes vos métriques d’évaluation mais sortez régulièrement la tête de vos chiffres pour observer votre agent sur sa politique optimale. Notez ces observations dans votre carnet d’entraînement : elles apportent potentiellement autant de valeur à vos expériences que vos métriques. Observer votre agent en situation vous permettra de repérer plus facilement les modèles qui n’ont aucune chance de converger (pour les éliminer) et vous en tirerez des conclusions intéressantes.
Nous avons répété ces expériences pour les mêmes indices d’exploration, mais en utilisant cette fois-ci la deuxième fonction de récompense. Les mêmes métriques que précédemment vous sont présentées ci-dessous.

On constate que les agents convergent bien plus vite (cf figure 5) : la fonction de coût décroît rapidement et se stabilise vers les 2000 étapes là ou 40 000 n’ont pas suffit avec la première fonction de récompense. Quelques pics indiquent que l’agent se trouve encore confronté à des situations nouvelles pour lesquelles il a besoin d’ajuster ses paramètres. L’évaluation des agents via la métrique de distance parcourue (cf figure 6) confirme également que cette deuxième fonction de récompense permet d’obtenir des performances bien plus intéressantes en termes de conduite autonome.
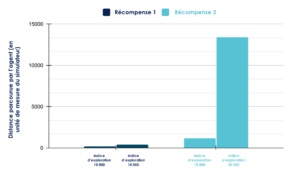
Les agents entraînés avec cette deuxième fonction de récompense sont parfois capables d’arriver au bout du circuit. Sur 20 essais (pour l’indice d’exploration de 30 000), tous semblent réussir à se tenir plutôt bien au centre de la route. Visuellement, l’agent est même capable de redresser sa trajectoire lorsqu’il se rapproche du bord de la route.
Nous avons observé qu’il était bien plus efficace de récompenser l’agent selon qu’il se rapprochait du centre de la route (fonction de récompense 2) que selon qu’il se trouvait plus ou moins proche du centre de la route (fonction de récompense 1). La nuance peut paraître fine, mais les effets sont loin d’être négligeables lors de l’entraînement.
Nous pensons qu’une explication réside dans l’assertion suivante :
La deuxième fonction de récompense modélise l’objectif “conduire de façon autonome” d’une manière moins ambiguë que la première fonction de récompense.
Reprenons nos deux fonctions de récompenses et tentons de comprendre pourquoi il est moins ambigu de dire :**“c’est une bonne chose pour conduire au centre de la route que de s’en approcher” (R2)plutôt que de dire :“c’est une bonne chose d’être au centre de la route, c’est un peu moins bien d’être légèrement excentré, c’est plutôt mauvais d’être au bord de la route” (R1)**Dans le cas de R2, l’agent obtient plus facilement l’information de “ce qu’il faut faire” : il faut se rapprocher du centre de la route. Dans le cas de R1, il obtient l’information qu’il est plus intéressant d’être au milieu de la route, mais il doit déduire tout seul qu’il faut tourner à gauche s’il est excentré sur la droite et inversement. Pour R2, l’information est “dynamique”, elle prend en compte l’action faite par l’agent sur un pas de temps et juge directement cette action. Pour R1, l’information est “statique” et ne fait qu’indiquer à l’agent la valeur de son état dans l’absolu, en ne donnant aucune information sur le genre d’action qui permettra de se retrouver plus souvent dans une situation “bonne” que “mauvaise” : cette information est moins exploitable.
Tip 5 : La fonction de récompense doit modéliser de façon la plus exploitable possible la question à laquelle vous souhaitez que votre agent soit capable de répondre.
Il est souvent difficile de choisir la fonction de récompense lorsque la question à laquelle on veut répondre n’a pas de réponse évidente. Prenez le temps d’écrire cette question et de formuler plusieurs réponses possibles. Pour cela, vous pouvez vous poser la question suivante :
En fonction de l’objectif que je cherche à atteindre, si l’on considère deux situations différentes (deux états différents) : quelle information permet d’arbitrer de façon la moins ambigüe possible si une action est bonne ou mauvaise ?
Notez que dans le cas de notre problème, il est assez facile de modéliser notre question : nous avons tous une idée de ce qu’est “bien conduire” dans la réalité ou dans un jeu vidéo. En fonction de votre cas d’usage vous aurez peut-être besoin d’aiguiser votre “connaissance métier”.
La fonction de récompense n’est bien évidemment pas le seul paramètre de votre algorithme. Il reste encore bien des paramètres à discuter que nous avons fixés sans vous en parler, quels sont-ils et comment les choisir ? Sans rentrer dans un catalogue d’expérience, nous allons maintenant vous exposer nos choix concernant les paramètres que nous jugeons les plus importants ainsi que quelques enseignements que nous en avons tirés.
L’espace des états est construit à partir d’une image fournie par le simulateur de la caméra frontale. Le traitement d’une telle image brute peut être exigeant en termes de ressources de calcul. Nous allons donc essayer de traiter cette image de façon à maximiser la valeur de l’information qu’elle contient par rapport à l’objectif de conduire de façon autonome, tout en minimisant le bruit - notamment l’information jugée inutile.
Ce pré-traitement a potentiellement une forte influence sur la durée d’apprentissage de notre algorithme ainsi que ses performances. Voici le pré-traitement que nous avons appliqué à l’image de la route pour construire notre espace des états :
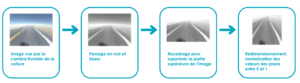
Tip 6 : Réduisez la taille de votre espace des états, mais pas trop. Tâchez d’y concentrer l’information qui vous paraît utile pour que votre agent prenne ses décisions.
Dans notre cas d’usage, l’image brute perçue par la caméra frontale de la voiture est une image en couleur. Cette caractéristique n’apporte pas de valeur pour savoir, dans une situation donnée, s’il faut tourner à droite ou à gauche (quelle importance que la ligne de la route soit jaune ou verte pour prendre cette décision ?). Passer l’image en noir et blanc semble donc une bonne idée pour réduire la taille de l’espace des états tout en conservant l’information utile sur l’image qui est grossièrement : ou sont les lignes de la route ? Plus factuellement, avec ce prétraitement on passe d’une taille de l’espace des états de (256x256x256)^(120x120) à 256^(120x120) (si la résolution de l’image est de 120 pixels par 120). Il est intéressant de réduire la taille de cet espace, mais attention, il ne faut pas trop la réduire non plus si vous avez choisi d’utiliser un réseau de neurones comme approximateur de votre fonction Q (ce qui est notre cas). Si la taille de cet espace est très faible, il faudra utiliser une table plutôt qu’un réseau de neurones (Blog Octo : L'apprentissage par renforcement démystifié).
Toutes ces transformations permettent de réduire la taille de l’espace des états et de minimiser le temps d’apprentissage de l’agent. Notre agent, en l’occurrence le réseau de neurones à qui on fournit les images, a donc un espace d'états plus petit et plus rapide à explorer. Parlons justement du réseau de neurones.
Souvenez-vous de notre premier article, le réseau de neurones est utilisé comme approximateur de la fonction Q. On lui présente une image pré-traitée de la route et on lui demande de prédire la valeur de chaque action possible pour l’état qu’il observe.
Il s’agit donc d’extraire de l’information à partir d’une image, et à ce petit jeu ce sont les réseaux de neurones convolutifs qui s’en sortent le mieux. Nous avons choisi d’utiliser une architecture de RNN très connue, popularisée par [Mnih et al., 2013].
Sans rentrer dans le détail de chacune des couches du réseau de neurones, les couches de convolution permettent notamment d’extraire des motifs récurrents issus des images données en entrées - typiquement des lignes, des courbes, etc. Pour s’en convaincre, observons les couches intermédiaires (ou feature maps) d’un réseau de neurones entraîné. Ces couches intermédiaires correspondent à des représentations plus “simples” des images qui sont données en entrée au réseau de neurones convolutif.

L’intérêt d’observer les couches intermédiaires est de gagner en compréhension sur l’information que le réseau de neurones cherche à extraire des images pour prédire avec plus de justesse la valeur de chaque action. Observez les images 8b et 8d : le réseau de neurones délimite les courbes de la route. On pourrait interpréter grossièrement cela par : “pour prédire s’il faut tourner à droite ou à gauche, le réseau de neurones cherche les limites de la route”.
Les images que l’on pré-traite et que l’on donne au réseau de neurones sont issues de notre simulateur. Il y a beaucoup à dire sur le simulateur et son paramétrage, nous nous concentrerons sur un aspect particulièrement important selon nous.
Le simulateur utilisé propose plusieurs environnements plus ou moins complexes en termes de textures, de couleurs ou de tracé de la route. Nous avons choisi l’environnement le plus simple dont un aperçu est donné en figure 8.
L’environnement de simulation génère plusieurs tracés de route, et choisit aléatoirement un tracé différent à chaque début d’épisode. Cet aspect de notre simulateur s’est avéré très important pour permettre à l’algorithme d’explorer correctement l’espace des états et de ne pas sur-apprendre sur un type de situation en particulier.
Tip 7 : Faites en sorte que votre agent rencontre le plus rapidement possible un maximum de situations différentes.
Cela peut paraître contre-intuitif, et à l’époque où nous n’avions pas d’algorithmes qui convergaient nous avions envisagé la stratégie suivante : s'entraîner d’abord sur une ligne droite, puis s’entraîner sur des virages et des courbes par la suite. Nous nous basions pour cela sur notre propre intuition : il paraît plus facile d’apprendre progressivement à conduire en commençant par une situation simple et de complexifier cette situation au fur et à mesure. C’est une erreur qui ne pardonne pas en apprentissage par renforcement, et pour comprendre pourquoi il faut rappeler ce qu’est le sur-apprentissage.
Le sur-apprentissage (ou overfitting) désigne la situation dans laquelle une fonction de prédiction est sur-adaptée aux données d’entraînement, donc inadaptée à se généraliser et à prédire correctement sur des données de validation (qu’elle n’a pas rencontré pendant sa phase d’apprentissage). Initialement théorisée pour l’apprentissage supervisé, cette notion peut s’élargir à l’apprentissage par renforcement si on considère que :
- Notre fonction à entraîner est le réseau de neurones ;
- Nos métriques d’apprentissage sont les états rencontrés par l’agent pendant l’apprentissage ;
- Nos métriques d’évaluation les états rencontrés par l’agent pendant la phase d’évaluation.
Autrement dit, si l’on s’entraîne d’abord sur des lignes droites, on a toutes les chances d’obtenir un réseau de neurones qui prédit tout le temps une valeur maximale pour l’action “aller tout droit” indépendamment de l’image qui lui est donnée en entrée. L’agent qui en résulte sera donc incapable généraliser et d’apprendre ensuite à tourner à droite ou à gauche.
C’est ce que nous avons constaté expérimentalement, des algorithmes entraînés toujours sur un même circuit commençant par un virage à droite on tendance à surestimer la valeur de l’action “aller à droite” et ne convergent jamais. Ces expériences ainsi que des exemples dans notre étude bibliographique [Vitelli and Nayebi, 2016] nous ont amené à comprendre qu’il était souhaitable de changer à chaque fois de circuit, en augmentant ainsi la diversité des situations dans la phase précoce d’apprentissage (là où l'algorithme est peu entraîné donc explore fortement).
N’oubliez pas que votre simulateur conditionne les états observés par votre agent. Au même titre que les paramètres de votre modèle, les paramètres de votre simulateur peuvent et doivent être ajustés.
Vous l’aurez compris, entraîner des algorithmes de RL comporte son lot de difficultés. Parmi celles que nous avons abordé dans cet article :
Pour réussir à les fixer :
Nous l’avons évoqué dans l’article précédent : ne sous-estimez pas la question de l’intégration du simulateur avec votre agent, vous aurez assez de paramètres à gérer pendant l’entraînement pour que le simulateur vienne s’en mêler. Accordez à cette question l’importance qu’elle mérite et tâchez de la résoudre le plus en amont possible. Une fois que votre environnement de simulation est fixé : on ne touche plus au simulateur et on cherche à améliorer le modèle.
Bonne chance :)
Vidéo de l'agent entraîné avec la fonction de récompense 2, pour un indice d'exploration de 30 000, en accéléré x4.
Article de Felix Yu : Train Donkey Car in Unity Simulator with Reinforcement Learning
Dilemme Exploration VS Exploitation
Blog Octo : L'apprentissage par renforcement démystifié
Wikipédia : les réseaux de neurones convolutifs
Towards Data Science : Visualising Filters and Feature Maps for Deep Learning
Overfitting et Underfitting : Quand vos algorithmes de Machine Learning dérapent