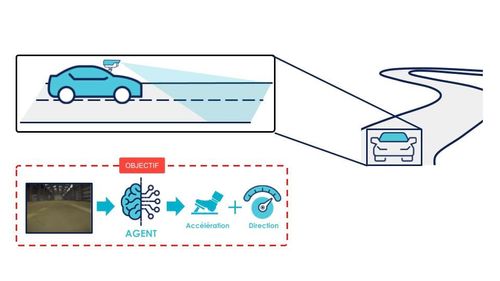
Afin d’explorer de nouvelles possibilités concernant la conduite autonome, de nombreuses compétitions de mini-voitures autonomes existent telles que la compétition de l’Iron Car ou encore la compétition Donkey ® Car aux États-Unis. Lors de ces compétitions, des mini voitures (type voitures radiocommandées) doivent parcourir quelques tours d’un circuit faisant approximativement la taille d’un hangar. Dans cet article, nous allons étudier l’utilisation d’une solution d’apprentissage par renforcement (RL - Reinforcement Learning - pour les intimes) pour la conduite autonome selon le contexte schématisé en figure 1.
Cependant nous n’irons pas jusqu’au déploiement en réel qui comporte son lot de complications (si vous voulez savoir quel(s) type(s) de complication(s) nous vous invitons à consulter l’article suivant : [Blog Octo : L'IA embarquée : entraîner, déployer et utiliser du Deep Learning sur un Raspberry (Partie 1)]).
Enfin, dans un deuxième article, nous entraînerons cet algorithme et nous analyserons les résultats en terme de conduite autonome.
Un précédent article sur le blog d’Octo [Blog Octo : L'apprentissage par renforcement démystifié] a déjà éclairci le sujet du RL dans les grandes lignes. Nous vous conseillons, si vous êtes novice dans le domaine du RL, de vous y référer pour vous familiariser avec les concepts les plus fondamentaux (principe général, notions d’état, d’action, de récompense et version basique du Q-learning) sur lesquels nous ne reviendrons pas ici. Dans le cas particulier de la conduite autonome :
L’apprentissage de l’agent dans l’environnement est résumé sur la figure 2.
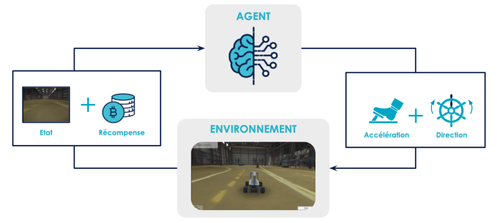
Nous avons choisi d’utiliser comme algorithme une “version améliorée” du Q-Learning décrit dans l’article précédent : le Deep Q-Learning. Pour rappel le but du Q-Learning [Watkins, 1989] est d’optimiser au fur et à mesure la fonction de valeur Q décrite en figure 3. Si on connaît cette fonction, alors on sait estimer correctement la valeur de chaque action pour un état donné et il suffit d’entreprendre à chaque fois la meilleure.
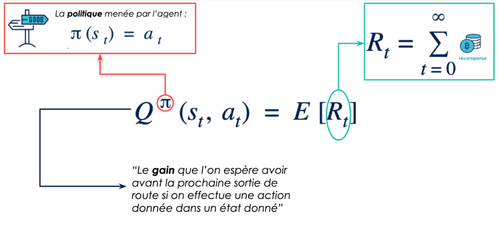
La notation pi (st)= at n’est pas totalement exacte. En réalité, la politique renvoie une distribution de probabilité des actions : pi(st) = p (at = a), pour tous les a dans A (l'espace des actions possibles), c’est à dire à quelle fréquence il faudrait effectuer chaque action dans telle ou telle situation. Cette dernière notation permet de décrire des cas plus complexes, par exemple au poker on peut imaginer qu’il est une bonne stratégie de bluffer parfois et on aurait donc une politique qui ressemblerait à p (at= "bluff") = 0.10 ; p (at = "se coucher") = 0.90 . On revient au cas décrit ici si la probabilité est de 1 pour une certaine action et de 0 pour toutes les autres.
Le Deep Q-Learning (DQL) [Mnih et al., 2013] propose comme approximateur de la fonction Q un réseau de neurones (généralement profond, d’où le terme Deep Q-Learning) plutôt qu’une Q-table comme décrit précédemment. Cela répond à la problématique de la taille de l’espace des états évoqué dans l’article précédent [Blog Octo : L'apprentissage par renforcement démystifié]. Dans notre cas, on choisit de décrire chaque état par une image de la route et après un prétraitement, cette image est en noir et blanc de taille 84 par 84. La taille de l’espace des états (noté S) dans ce cas est donc |S| = 256^(84x84) ≈ 1O^(16 992) , ce qui est bien trop grand pour autoriser une représentation de la fonction de valeur Q sous forme de tableau (qui aurait donc 1O^(16 992 lignes)).
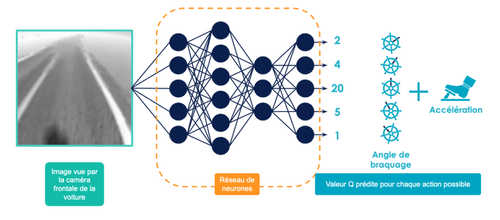
Il s’agit ici de comprendre que l’on veut utiliser un réseau de neurones comme un “oracle” que l’on consulte. On lui présente une image de la route et il nous indique pour chaque action possible la récompense totale que l’on est censé obtenir avant de sortir de la route (i.e. avant la fin de l’épisode) comme le montre la figure 4. Bien entendu cet oracle n’est pas pertinent au début de l’entraînement car on choisit en général des poids aléatoires quand on initialise un réseau de neurones mais on va l’entraîner et ce quasiment de la même façon que l’on mettait à jour notre Q-table.
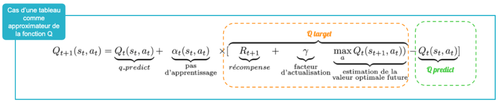
Si l’on change la représentation de notre fonction de valeur Q, on doit également changer notre méthode de mise-à-jour lors de l’entraînement. Souvenez-vous de l’équation de Bellman décrite dans l’article précédent et rappelée en figure 5, elle permet de remplacer une valeur par une autre en fonction de la récompense obtenue pour affiner l’estimation.

Si les termes de descente de gradient et de fonction de coût ne vous sont pas familiers, vous pouvez vous référer à l’article suivant [Blog Octo : Classification d’images : les réseaux de neurones convolutifs en toute simplicité], notamment le paragraphe “Entraînement des CNN, quelques principes”. Il n’est cependant pas nécessaire ici de connaître en détail le fonctionnement, seulement de comprendre qu’un réseau de neurones possède des valeurs numériques qui lui sont propres (appelées poids) et qui lui servent à prédire ses valeurs de sorties à partir de ses entrées. Ce sont ces valeurs qui sont modifiées lors de l’apprentissage. Pour les modifier, on utilise une métrique : la fonction de coût. Cette fonction de coût est un indicateur basé sur la différence entre les valeurs actuellement prédites par notre réseau de neurones et celles que l’on voudrait qu’il prédise. En Deep Q-Learning on utilise la fonction de récompense pour calculer les valeurs que l’on souhaite que notre réseau de neurones prédise. Le gradient est un vecteur qui contient la modification des poids à effectuer pour tendre vers cet objectif et affiner notre prédiction. Effectuer une “descente de gradient” c’est donc répéter ce mode de fonctionnement autant de fois que nécessaire afin que les paramètres du réseau de neurones s’affinent progressivement pour prédire pertinemment les valeurs cibles.
Le principe reste donc le même que précédemment, à chaque mise-à-jour des paramètres de notre réseau de neurones, le réseau “tend un peu plus vers” une estimation correcte de la fonction de valeur Q. On peut donc supposer que si on s’entraîne suffisamment longtemps le réseau de neurones va converger et l’estimateur va devenir bon.
En réalité la convergence de tels algorithmes n’est pas mathématiquement prouvée. Celle-ci a été démontrée dans le cas d’utilisation d’approximateurs linéaires de la fonction de valeur Q (telles que les Q-tables) [Watkins and Dayan, 1992] mais pas en utilisant des approximateurs non-linéaires tels que les réseaux de neurones. N’ayez crainte, le succès de l’utilisation de ces méthodes laisse à penser qu’ils convergent, sans que l’on sache encore exactement pourquoi...
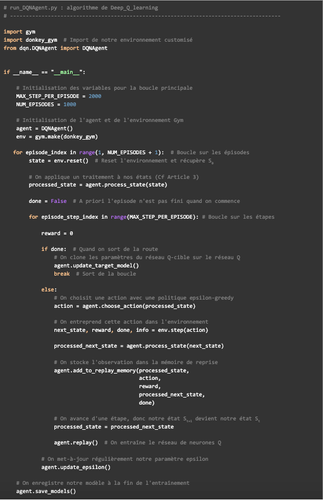
En prenant en compte tout ce qui vient d’être dit l’algorithme du DQL est :

Cependant, le DQL ainsi implémenté est considéré comme instable lorsqu’il utilise des approximateurs non-linéaires tels que les réseaux de neurones profonds [Tsitsiklis and Van Roy, 1997]. Cela est principalement dû à deux choses :
Afin de traiter le premier problème #1, une méthode appelée experience replay peut être utilisée.
Le principe de l'experience replay [Lin, 1992] est d’utiliser une mémoire de reprise (replay memory) pour stocker les transitions observées lors de l’exploration de l’environnement de la part de l’agent puis les sélectionner aléatoirement à chaque étape de l’apprentissage. Ces tuples de transitions sont des quintuplets de la forme (st, at, rt, st+1, terminalt) (terminal étant un booléen indiquant si l’état est terminal ou non) correspondant à une seule étape de l’exploration de l’environnement. Lors de l’étape de mise à jour des paramètres du réseau de neurones, on sélectionne aléatoirement les expériences à l'intérieur de cette mémoire de reprise plutôt que de s’entraîner sur la dernière expérience observée ce qui évite d’introduire un biais lors de l’apprentissage. Ce principe est résumé en figure 8.
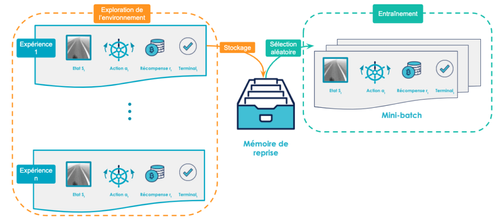
Un deuxième avantage de cette technique est qu’elle donne la possibilité de s’entraîner par “lots” (mini-batches) et de pouvoir faire une descente de gradient stochastique. Sans rentrer dans le détail, plutôt que de mettre à jour les paramètres de notre réseau de neurones en n’utilisant qu’une seule étape de transition à chaque fois, on calcule un gradient “agrégé” qui moyenne plusieurs gradients issus de plusieurs étapes de transition différentes. Cette technique permet d’augmenter les chances de trouver “une bonne direction” pour la descente de gradient et d’augmenter la vitesse de convergence de l’algorithme [StackExchange : "Shuffling data in the mini-batch training of neural network"].
Reste un deuxième problème à résoudre : la forte influence de la fonction Q sur la politique menée et donc sur la distribution des états rencontrés dans l’environnement #2.
Le Double Deep Q-Learning (DDQL) est une version améliorée du DQL permettant de palier à l’une de ses faiblesses : la surestimation de l’importance de certaines actions dans certaines conditions [van Hasselt et al., 2015].
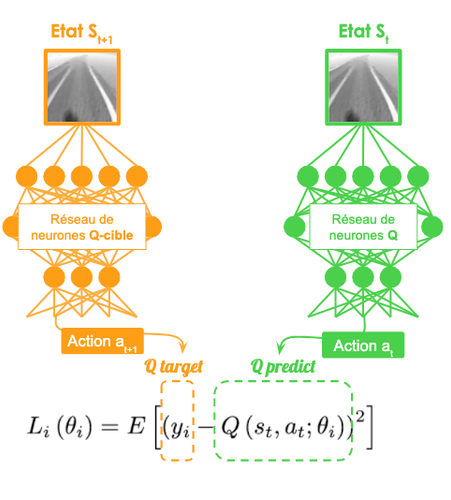
L’idée derrière le DDQL est de séparer la sélection de l’action qui maximise la valeur Q de son évaluation. L’expression de mise-à-jour de la valeur Q donnée dans l’expression de la fonction de coût utilisée pour la descente de gradient sur le réseau de neurones suppose l’utilisation du même réseau de neurones pour sélectionner l’action at+1 et pour calculer la valeur Q (st+1, at+1, theta(actuel)). Le DDQL propose donc l’utilisation de deux réseaux de neurones distincts :
Lors de l’entraînement, les paramètres du réseau de neurones "Q-cible" sont régulièrement mis-à-jour en clonant les paramètres du réseau de neurones "Q" ce qui permet de profiter de l’amélioration de l’estimation dû à l’apprentissage progressif de l’agent pendant l’entraînement.
Le pseudo code de notre algorithme de DDQL avec expérience-replay s’écrit comme suit :

Nous avons décrit le type d’algorithme utilisé et son fonctionnement. Mais concrètement comment cet algorithme interagit avec le simulateur ?
Un simulateur de conduite est a priori un jeu vidéo conçu pour interagir avec un utilisateur humain via une interface physique. Pour pouvoir être manipulé par un agent de RL, le simulateur doit posséder une API [Application Programming Interface] permettant un appel automatisé aux commandes du simulateur. Si cette API n’est pas directement incluse dans le code du simulateur, il faut concevoir une couche supplémentaire de code, un wrapper, permettant de remplir cette fonction.
Nous avons introduit dans l’article précédent une API standard souvent retrouvée dans le domaine du RL : l’interface [Gym]. Pour répondre à notre problème nous allons devoir créer un environnement personnalisé qui ressemble à ceci :
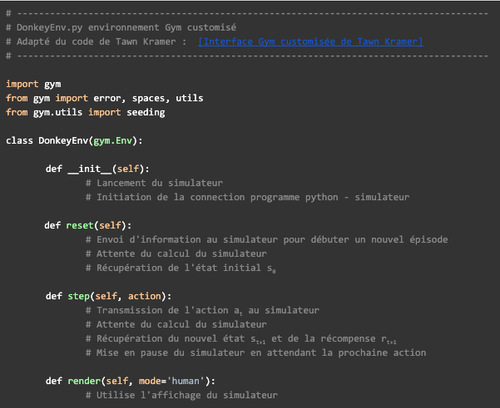
Pour notre cas d’usage, nous allons utiliser le simulateur Donkey Car dans sa version proposée par Tawn Kramer [Code source du simulateur Donkey de Tawn Kramer]. Ce simulateur est un code source écrit en C# qui, compilé à l’aide du logiciel d’édition de jeux vidéos 3D Unity, permet de générer un fichier binaire. Pour interagir avec le processus correspondant à l’exécution de ce fichier binaire, nous utilisons une interface Gym customisée selon le modèle décrit précédemment (reconstruite à partir de celle de Tawn Kramer [Interface Gym customisée de Tawn Kramer]). C’est dans l’implémentation des classes et méthodes de cette interface qu’on gère la communication avec le simulateur via le réseau local. Par la suite, nous utiliserons le terme de simulateur pour désigner l’ensemble formé par le fichier binaire compilé à l’aide d’Unity ainsi que le wrapper Python (implémentation de l’interface Gym customisée) comme résumé en figure 12.
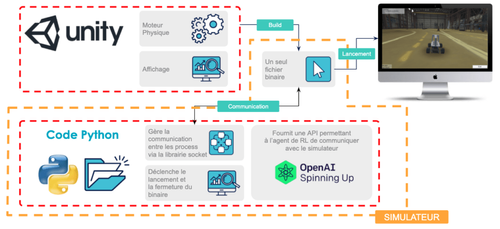
Mettre en place cet environnement n’est en réalité pas une mince affaire. Il faut apporter des modifications aux codes sources cités desquels nous sommes repartis, mais de telles considérations nous emmeneraient en dehors du sujet de cet article. Ici, il s’agit simplement de comprendre que nous nous sommes outillés d’une librairie Python customisée nous fournissant toutes les méthodes utiles à l’interaction de notre algorithme avec notre simulateur.
Nous avons décrit l’algorithme de Double Deep Q-Learning utilisé, ainsi que les modalités de son interaction avec le simulateur. Ce qu’il est important de retenir :
Le pseudo code de notre algorithme est donné en annexe 1.
Il est important de remarquer que la seule chose qu’est capable de faire un algorithme de RL est de converger vers la politique maximisant la récompense. Si l’entraînement fonctionne bien, l’algorithme va trouver une manière (si ce n’est la meilleure) d’évoluer dans l’environnement pour maximiser la récompense. Cependant si la maximisation de cette récompense n’a aucun rapport avec la tâche que nous souhaitons accomplir… l’algorithme convergera vers un état où il est incapable de remplir sa tâche. N’ayez crainte, nous aborderons la question du choix de la fonction de récompense dans l’article suivant.
Notre environnement d’apprentissage et notre algorithme étant prêt, on peut commencer l’entraînement … ce que nous verrons dans un deuxième article !