Le premier article était consacré à la structure et au fonctionnement des algorithmes évolutionnistes et le second portait sur leur performance.
Nous allons ici nous intéresser à un cas d'application concret d'algorithmes évolutionnistes sur un problème de données complexes. Le cas d'application présenté est l'utilisation d'un algorithme évolutionniste comme une alternative à de l'apprentissage par renforcement pour entraîner un véhicule à se déplacer dans un environnement simulant un circuit. Le problème s'apparente ici à celui de la conduite autonome.
L'apprentissage par renforcement avait été brièvement évoqué dans le second article, plus particulièrement l'aspect inverse du fonctionnement global de l'apprentissage par renforcement comparativement à l'utilisation d'algorithmes évolutionnistes :
Les algorithmes évolutionnistes peuvent être utilisés pour entraîner des modèles de décision. L’évolution du modèle se fait en modifiant le modèle et en conservant les évolutions améliorant la performance, alors que pour l'apprentissage par renforcement ce sont les performances qui entraînent les modifications du modèle (on cherche à corriger les défauts et conserver ce qui est correct).
fig 1 : Fonctionnement comparatif entre les algorithmes évolutionnistes et d’autres techniques d'apprentissage
Plus particulièrement, le renforcement est un des paradigmes de machine learning où l'on ne dispose pas de données mais d'un environnement avec lequel va interagir un agent. La donnée est donc générée au fil de l'apprentissage, chaque action prise dans l'environnement par l'agent générant un nouvel état. L'environnement va aussi donner une information sur la qualité des actions effectuées via un mécanisme de récompenses. Le but de l'agent est alors de maximiser sa récompense.
Si vous souhaitez avoir plus d'informations sur l’apprentissage par renforcement, je vous invite à lire les 2 articles du blog qui traitent spécifiquement de leur application dans l’apprentissage de la conduite autonome (disponibles ici ) ; ils peuvent aussi vous donner une autre vision de ce problème !
L'apprentissage par renforcement permet aujourd'hui d'atteindre des résultats exceptionnels sur de nombreux problèmes, en particulier sur de nombreux jeux comme le Go ou les échecs 1, pour autant, plusieurs recherches 2 3 ont pu mettre en avant le fait que les algorithmes évolutionnistes peuvent être une alternative au renforcement pour entraîner des IA sur ces mêmes problèmes.
La conception de notre modèle est relativement simple, on dispose de 3 éléments: l'environnement, une intelligence artificielle (IA) et l’agent : la “voiture” elle-même (l’objet qui va se déplacer dans l’espace). À chaque pas de temps:
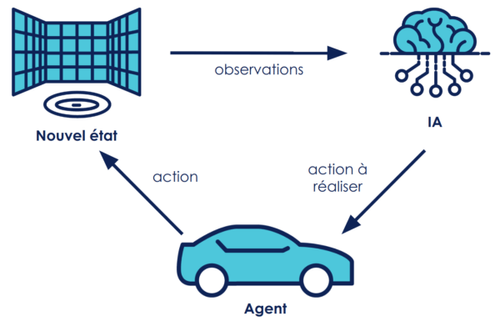
Pour l'entraînement on ajoute une caractérisation de l’action (score donné à l’action qui définit si l’action réalisée était bonne ou mauvaise).
Un des choix critiques à faire pour notre modèle est celui de l’environnement dans lequel on va l'entraîner. On veut que cet environnement respecte plusieurs conditions:
En pratique, le monde réel se prête assez mal à l'entraînement de notre modèle.
En conséquence, le choix s’est porté sur l’utilisation d’un environnement virtuel pour entraîner notre modèle.
Les environnements virtuels disposent de nombreux avantages par rapport au monde réel :
Il existe de nombreuses solutions pour créer des environnements virtuels. En particulier, les moteurs de jeux fournis par certains éditeurs permettent de facilement créer des environnements.
Le choix s’est porté sur l’utilisation de Unity pour différentes raisons, la principale étant que Unity dispose d’un module : ML-agents 1, spécifiquement créé pour l'entraînement d’intelligences artificielles dans des environnements virtuels et contrôlable directement avec du code Python.
Notre environnement virtuel est composé de 2 éléments principaux :
Notre agent (le véhicule) est constitué:
fig 3 : Un environnement virtuel dans l'éditeur de Unity
L’agent, représenté par le cube rouge, peut se déplacer librement dans le plan horizontal de l’environnement.
L’environnement exclut toute force pouvant s'exercer sur l’agent à l’exception des commandes directionnelles (accélération et rotation) et d’une force de frottement constante (qui représente les différents frottement subis par l’agent).
Une expérience se poursuit tant que l’agent ne quitte pas le circuit (le tracé blanc) ou ne dépasse pas le nombre maximal d’épisodes autorisées (une action à réaliser étant demandée à chaque épisode / pas de temps).
A chaque pas de temps, l’environnement transmet au travers du connecteur ML-agents une image vue par une caméra fixée sur l’agent, et se fige en attendant une action à réaliser. Une fois une action envoyée, l’environnement exécute l’action et renvoie l'image de la caméra (de taille 21*32 pixels en nuances de gris) correspondant au nouvel état. La résolution est la taille de l’image ont été choisies pour limiter leur taille en conservant une résolution convenable pour limiter la taille du modèle que l’on va utiliser.

Fonctionnement de l’intelligence artificielle
Pour ce problème, le choix s’est porté sur l’utilisation d’un réseau de neurones pour contrôler les actions de notre agent. Notre modèle (ie le réseau de neurones) est constitué de 2 couches de convolutions et de 2 couches complètement connectées, à l'architecture suivante:
fig 5 : structure du réseau de neurones utilisé
Le réseau possède environ 980 000 paramètres répartis dans les différentes couches. Le choix du réseau a été fait arbitrairement tant au niveau de sa structure (inspirée de réseaux convolutifs simples classiques), que du nombre de neurones sur chaque couche (à l’exception du nombre de paramètres en entrée et en sortie).
Notre réseau prend en entrée non pas 1 mais 3 images, qui correspondent à 3 pas de temps successifs de l’agent. Autrement dit, si l’agent se trouve à un instant T, on va fournir en entrée les images vues par la caméra aux instants T, T-1 et T-2.
Ce choix est fait pour des considérations physiques :
En fournissant à l’agent uniquement l’image à l’instant T : il est en mesure de connaître sa position dans l’espace mais incapable de connaitre sa vitesse ou son accélération. Avec 2 images, on peut connaître sa position dans l’espace et donc déduire sa vitesse (dérivée de l’espace par rapport au temps, le pas de temps étant fixé). De façon analogue à l’obtention de la vitesse, on peut trouver l’accélération en connaissant la vitesse à 2 pas de temps successifs. Pour connaître les 3 paramètres du mouvement, on a donc besoin d’au moins 3 images, d’où ce choix de conception.
Chacun des 9 neurones en sortie est associé à une action et l’action dont la valeur en sortie du neurone est maximale sera exécutée. Les actions que j’ai choisi de considérer pour le problème sont les suivantes :
fig 6 : liste des 9 actions possibles
L’environnement maintient à jour 2 paramètres : vitesse et direction de l’agent. Avancer et freiner font varier cette vitesse, les virages changent la direction. “ne rien faire” ne signifie donc pas que l’agent reste immobile (il conserve sa vitesse et sa direction et subit encore la force de frottement qui le freine).
Dans le problème de conduite autonome, on cherche à entraîner notre réseau de neurones, autrement dit, à modifier les poids du réseau pour qu’il puisse piloter notre agent de façon efficace. On peut donc représenter chaque individu directement par un réseau de neurones, les poids du réseau étant les paramètres qui vont être modifiés : tous les individus ont le même réseau de base (structure du réseau identique) mais les valeurs des paramètres (les poids) de ce réseau vont varier.
En particulier, c’est sur les poids du réseau que l’on va appliquer notre algorithme évolutionniste. Pas de backpropagation ou descente de gradient ici donc.
L’idée est que nos circuits ont une structure cyclique : lorsque l’on fait un tour complet, on revient à son point de départ. Autrement dit, faire un tour autour d’un circuit sans croisement revient à faire un tour à 360° autour du centre du circuit. A chaque pas de temps (entre l’instant T et T+1) on peut donc trouver l’avancement angulaire ΔӨ autour du circuit :
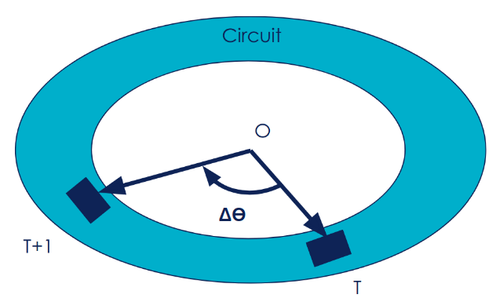
On peut donc définir à chaque pas de temps une récompense de l’action comme étant l’angle orienté ΔӨ d’avancement entre les position à l’instante T et T+1 par rapport au centre O du circuit. La récompense de l’action exécutée à l’instant T entre T et T+1 vaut donc :
RT➝T+1 = Δθ
Le score d’un individu (sa fitness) sur l’expérience peut alors se définir comme la somme des récompenses de chaque pas temps sur toute l’expérience :
Fitness = Σ RT➝T+1
Un individu qui exécute un tour complet aura donc une fitness de 360, une moitié de tour, … alors qu’un individu qui irait en marche arrière aurait un score négatif, l’ange étant orienté.
L’objectif étant de juger les performances d’un algorithme évolutionniste sur ce problème, c’est donc avec cette méthode que l’on va entraîner notre réseau de neurones.
J’ai utilisé une population de 30 individus - pour limiter le nombre de calculs nécessaires à réaliser - et le nombre maximal d’épisodes autorisés par expérience est de 4000 pas de temps.
Initialisation
On initialise les poids du réseau de chaque individu de façon aléatoire.
Méthodes d’évolution
Le croisement entre un individu A et B se fait de la façon suivante, pour chaque poids dans le réseau on a :
- 80% de chance de prendre le poids de l’individu A. - 20% de chance de prendre le poids de l’individu B.
la mutation :
- chaque poids à 10% de chance de se faire modifier selon une gaussienne normale réduite avec un écart type de 0.1.
Lors de l’étape d’évolution on génère une sous population d’individus de la façon suivante :
On sélectionne aléatoirement 2 individus de la population (avec une pondération sur leur fitness) pour générer un nouvel individu via une opération de croisement. Ensuite, on effectue une étape de mutation sur ce nouvel individu.
Sélection
A chaque génération, pour une population de parents de taille n (ici n=30), on génère n-1 enfants. On conserve à la fin de la génération les n-1 enfants ainsi que l’individu le plus performant de la population initiale (parents).
Cette approche permet de conserver l’individu le plus performant rencontré depuis le début de l’expérience.
On utilise ici un seul circuit où sont répartis des obstacles variés de façon progressive, assez peu complexes au départ (petit virages uniquement) pour se complexifier au fil du circuit (épingles, angles droits, ...),
En plus de ce premier circuit, un second circuit a aussi été généré pour estimer la capacité de généralisation de notre modèle. Il a pour but de vérifier si notre modèle était optimisé uniquement sur un unique circuit (celui d'entraînement) ou s’il est en mesure de généraliser à d’autres circuits.
Il n’est pas question ici à proprement parler d'overfitting tel que l’on peut le retrouver sur les problèmes de données classiques. En effet, on n’entraîne pas notre modèle sur un circuit particulier (les poids du réseau sont modifiés de façon aléatoire par les méthodes d’évolution): on ne fait que vérifier la performance des individus sur un circuit particulier. Techniquement, le circuit “d’entraînement” est donc déjà en lui-même un circuit de test. En revanche, on peut attester de la capacité de généralisation de chaque individu: est-il performant sur un seul circuit / type de circuit ou sur plusieurs ?


J’ai lancé plusieurs expériences avec l’algorithme, voici les résultats obtenus pour 2 d’entre-elles :
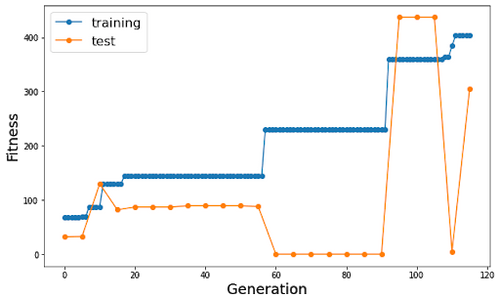
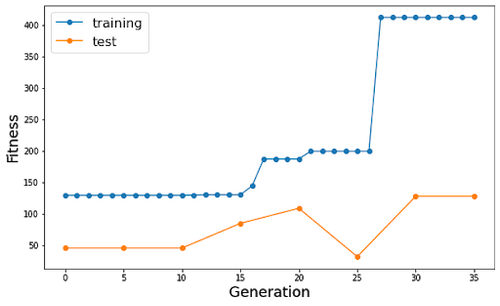
La courbe bleue représente la fitness du meilleur individu de la génération (et donc du meilleur individu jusque là) sur le 1er circuit, la courbe orange la fitness de ce même individu sur le 2ème circuit.
On observe bien que la fitness maximale augmente par paliers au fil des générations sur le circuit d’entraînement (le meilleur individu étant retenu, la courbe avance bien par paliers).
L’algorithme est bien en mesure de progresser sur notre problème de conduite : on parvient, plus ou moins rapidement en fonction des itérations, à aboutir à un individu qui est en mesure de parcourir le circuit en entier. En effet, à partir d’un certain seuil, les individus sont arrêtés non pas par contact entre la bordure du circuit et l’individu mais par le nombre maximal d’épisodes autorisés et parviennent à faire plus d’un tour.
Comparativement, en faisant manuellement des tests sur le premier circuit, j’ai pu obtenir avec les 4000 épisodes autorisés un score de 480, à comparer au meilleur obtenu qui est de 411, cela correspond donc environ à une performance 25% inférieure.
Notre modèle permet donc d’entraîner efficacement l’agent à circuler sur le circuit d’entraînement. En revanche, la capacité de généralisation du modèle reste limitée : si de meilleures performances sur le 1er tendent à donner de meilleurs résultats aussi sur le second, ce n’est pas toujours le cas, comme on peut le voir certains individus qui parviennent à parcourir plus d’un tour sur le premier circuit restent immobiles sur le second (cf. figure 10 courbe de gauche génération 110) quand d’autres sont capables d’être très performants sur les 2 (cf. courbe de gauche génération 100).
En modifiant la résolution de l’image d’entrée du réseau, la taille du réseau ou en changeant les paramètres de l’algorithme (taille de la population, méthodes d’évolution et de sélection), on pourrait espérer obtenir de meilleurs résultats. La structure du réseau tout comme les méthodes d’évolution n’ont en effet pas fait l’objet de recherches poussées dans cet exemple et ont été choisies arbitrairement.
Dans l’ensemble, la méthode peut permettre d’obtenir des résultats très satisfaisants (cf. l’individu de la 100ème génération de la première itération performant bien sur les 2 circuits), les différences de vitesse de progression entre les différentes itérations étant principalement imputables à la taille limitée de la population (certaines expériences bénéficiant de conditions initiales plus favorables).
Dans l’ensemble, compte tenu de la taille réduite de la population sur les expériences, des choix arbitraires au niveau des méthodes d’évolution et de la structure du réseau, les résultats sont intéressants : notre modèle possède près d’1 million de paramètres et on parvient en quelques dizaines d’itérations avec 30 individus à obtenir des performances remarquables.
Comme mentionné initialement, il est envisageable de substituer complètement un algorithme évolutionniste à des méthodes de renforcement et obtenir des résultats très satisfaisants 2 3. Mais une utilisation intéressante qui peut être faite des algorithmes évolutionniste est en couplage avec d’autres méthodes plus efficaces pour de l’optimisation locale : L’algorithme évolutionniste permet d’explorer avec une excellente efficacité des espaces solution très larges (ici 1 millions de paramètres) et de s’approcher rapidement d’optima locaux. En revanche il est plus difficile de converger sur un optimum une fois ce dernier localisé, à l’inverse des méthodes traditionnelles de renforcement qui mettent souvent un temps non négligeable pour obtenir des progrès significatifs mais qui s’affranchissent de ces phénomènes "paliers" et convergent plus rapidement une fois proche d’un optimum.
On pourrait donc envisager une structure où l'on utiliserait d’abord un algorithme évolutionniste pour se rapprocher d’un optimum local avant d’utiliser une autre méthode (renforcement,... ) pour converger plus finement vers l’optimum.
J’ai présenté ici l’utilisation d’un algorithme évolutionniste sur un problème classique propice à l’apprentissage par renforcement.
Sa mise en place de l’algorithme est assez simple une fois l’environnement généré (il suffit d’implémenter les méthodes d’évolution, de sélection, et une méthode pour communiquer avec l’environnement).
On a vu qu’il était possible d’obtenir des résultats avec des performances remarquables en fonction des itérations avec des configuration non optimisées (population de 30 individus pour 1 million de paramètres).
Le fait d’utiliser un unique circuit peut être vu comme un gage de simplicité de mise en place mais peut amener à un manque de généralisation : les algorithmes évolutionnistes sont des algorithmes d’optimisation et comme on peut le voir avec les résultats obtenus, 1 circuit n’est pas omnipotent.
Néanmoins, les capacités de généralisation de l’algorithme existent (certains individus performent de façon exceptionnelle sur plusieurs circuits comme on a pu le voir) ou peuvent être mises en place : utilisation de plusieurs circuits, …
En particulier, on peut envisager un véritable intérêt aux algorithmes évolutionnistes dans un fonctionnement couplé avec d’autres algorithmes d’optimisation comme l’apprentissage par renforcement. On laisse alors la partie exploratoire initiale à un algorithme évolutionniste qui va permettre d’obtenir une sorte de modèle de base avec des performances potentiellement non optimales mais pas complètement aléatoires. Base sur laquelle on va pouvoir ensuite lancer le second algorithme plus prompt à optimiser finement les performances.
Voici le meilleur résultat obtenu sur le circuit de validation (correspondant à la génération 100 de la première itération de l’algorithme) pour illustrer le résultat final obtenu :
[video width="900" height="auto" mp4="http://blog.octo.com/wp-content/uploads/2021/05/video-1.mp4][/video]
fig 11 : vidéo de l’agent le plus performant sur le circuit de validation avec l’image vue par la caméra de l’agent (g) et la réalité (d)
Références