Nous avons pu voir dans la première partie les différents éléments constitutifs d'un algorithme évolutionniste et quelques cas d’utilisations classiques des algorithmes évolutionnistes avec des applications à des problèmes de données.
Pour autant, ces algorithmes sont-ils compétitifs face aux autres types d’algorithmes d’optimisation ? Sur quels types de problèmes sont-ils les plus efficaces ? Cette partie vise à analyser les performances des algorithmes évolutionnistes ainsi que les facteurs qui affectent cette performance, le tout au travers d’un exemple concret.
En 1997 Wolpert et Macready ont publié un article [1] où ils explicitent l’existence de théorèmes, les No Free Lunch Theorems, qui permettent de relier les algorithmes aux problèmes qu’ils cherchent à résoudre. En particulier, un des théorèmes peut se résumer de la façon suivante:
No Free Lunch Theorem : 2 algorithmes sont équivalents en performance en moyenne à travers l’ensemble des problèmes possibles.
Autrement dit, comme illustré dans le schéma ci-dessous, un algorithme très performant sur un problème ou une classe spécifique de problèmes d'optimisation, va payer cette performance sur les autres problèmes. Entre autres, l’algorithme "aléatoire" est donc en moyenne aussi performant que les autres algorithmes sur l’ensemble des problèmes.
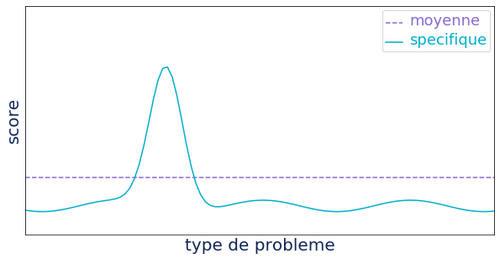
Toutefois, sur certains types de problèmes ou dans certaines conditions, il est possible de tirer parti au maximum d’un algorithme évolutionniste par rapport à un autre algorithme d’optimisation. Notamment quand l’espace de recherche est connu, les algorithmes évolutionnistes peuvent s’avérer moins performants car ils ne tirent pas parti (hors initialisation de la population) des connaissances préalables de l’espace. En revanche si l’espace de recherche est assez peu connu / compris, les algorithmes évolutionnistes sont particulièrement intéressants, d’autant plus si l’on ne cherche pas la solution optimale mais qu’une solution approchée est suffisante.
Les algorithmes évolutionnistes ont aussi l’avantage, comme les autres algorithmes basés sur une population, d’être performants sur les espaces fortement non convexes (avec beaucoup de maximum locaux par exemples) grâce à la multiplicité de la population, on limite ainsi le risque de rester bloqué dans un optimum local à cause des conditions initiales, en répartissant les individus dans l’espace solution.
En revanche, les algorithmes évolutionnistes sont très gourmands en temps de calcul: la fonction de fitness (qui évalue les individus) peut demander un nombre important de calculs (test -avec entraînement éventuellement- de réseaux de neurones par exemple). Toutefois, l’accès au cloud et à la parallélisation permettent de mettre en place ce genre de calculs avec une infrastructure adaptée.
Un problème qui apparaît dans les problèmes d’optimisation et de machine learning est le fléau de la dimension.
Le fléau de la dimension décrit le fait que la taille de l’espace explorable augmente exponentiellement avec la dimension. Cela se traduit entre-autres par le fait que l’exploration de l’ensemble de recherche devient trop coûteuse avec une augmentation du nombre de paramètres. Par exemple si on cherche à entraîner un réseau de neurones avec 1000 paramètres, on ne peut pas tester toutes les combinaisons de poids possible (même en restreignant les poids à 2 valeurs on arrive à plus de 10^301 configurations possible). Dès lors, une des questions qui se pose souvent sur des problèmes d’optimisation est la question du compromis entre exploration (explorer l’espace pour chercher de nouvelles zones performantes) et exploitation (se focaliser sur les zones que l’on sait performantes).
Le rapport entre les 2 pondère le rapport entre le coût et la performance.
En pratique, la sélectivité (méthodes de sélection des individus) ainsi que la taille de la population jouent un rôle primordial sur cet aspect, plus la population est importante et la sélectivité est faible, plus l’algorithme se place dans une optique d’exploration.
J'ai mentionné que les algorithmes évolutionnistes étaient particulièrement intéressants sur des problèmes complexes à forte dimensionnalité (type NP-complets comme le problème du voyageur de commerce). Ils permettent notamment une convergence assez rapide vers une solution approchée sans avoir besoin de parcourir l’ensemble de l’espace de solutions et offrent de nombreux moyens pour gérer le dilemme exploration / exploitation, entre-autres:
On avait mentionné précédemment le No Free Lunch Theorem qui rend difficile la comparaison entre différents algorithmes du fait de la spécialisation possibles de certains algorithmes. On peut néanmoins remarquer qu'avec leur structure d’évolution successive, les algorithmes évolutionnistes ressemblent particulièrement à l’apprentissage par renforcement où là aussi l’individu est modifié de façon itérative. Si l’apprentissage par renforcement forme aujourd’hui l’état de l’art sur un certain nombre de problèmes, les chercheurs d’OpenAI et Uber AI ont montrés que des algorithmes évolutionnistes pouvaient atteindre des performances proches ou équivalentes à des algorithmes par renforcement [1][2] avec certains avantages notables.
Notamment, ils ont pu observer que les algorithmes évolutionnistes:
En revanche, la quantité de calcul à réaliser peut être de l’ordre de 3 à 10 fois plus importante que par renforcement (à pondérer avec la parallélisation possible).
On peut résumer la différence entre le machine/deep learning classique et les algorithmes évolutionnistes avec le schéma suivant :
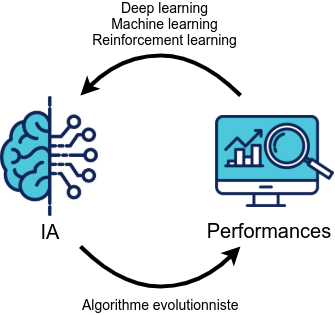
Le machine / deep learning classique est dans une approche d'amélioration par rapport au résultat, autrement dit, ce sont les performances de l'IA (réseau de neurones, ...) qui vont entraîner les modifications : on va chercher à corriger les erreurs et conserver exact ce qui l'est. Un algorithme évolutionniste suit le sens inverse : ce sont les modifications de l'IA qui vont entraîner les modifications des résultats et on va donc conserver les modifications utiles / performantes.
Pour illustrer un peu le fonctionnement d’un algorithme évolutionniste et l’impact du paramétrage et de la représentation, on va s’intéresser dans l’exemple à l’optimisation d’une fonction inspirée de la fonction de Ackley :
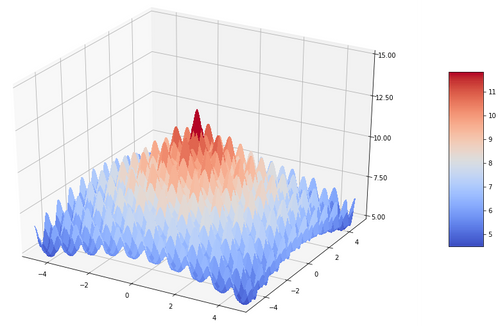
L’objectif ici est d’approcher le maximum de la fonction qui se trouve (0,0) et vaut: 10+e ≃ 12.718.
On va comparer ici 3 algorithmes différents qui ont été choisis de tel sorte à être différent entre-eux sur certains aspects spécifiques (sélection ou représentation - et donc méthodes d’évolution-):
Algorithme 1 :
Algorithme 2 :
Algorithme 3 :
On réalise 10 itérations de chaque algorithme avec 2 tailles de population différentes (5 et 50) sur 200 générations. Les individus sont tous initialisés aléatoirement avec x et y entre -5 et 5. Chacune des courbes de chaque graphique représente 1 itération.
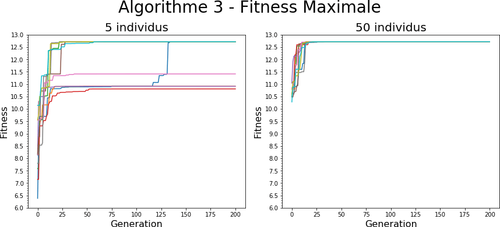
Comme on peut le voir en observant les courbes de fitness maximale pour des populations de 5 et 50 individus sur l’algorithme 3, on peut observer que la taille de la population peut avoir un impact important sur la qualité de l’optimum qui est atteint. Cela coïncide avec l’idée qu’une plus grande population permet une plus grande exploration initiale et augmente donc les chances de trouver un meilleur optimum (cf. dilemme exploration / exploitation). Cet aspect reste néanmoins à relativiser en fonction de l’algorithme et du problème, l’impact de la taille de la population pouvant varier.
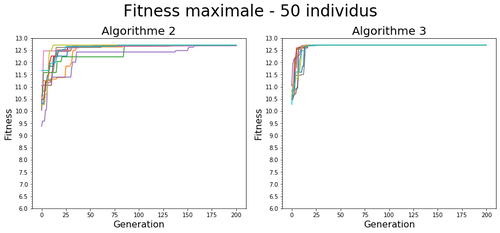
Les algorithmes 2 et 3 ne diffèrent que par leur méthode de sélection. En prenant aussi en compte la génération précédente (parents) en plus des enfants au moment de sélectionner les individus qui peuvent survivre à la génération suivante, l'algorithme 3 est plus sélectif que l'algorithme 2. Il favorise une forme d'inertie de la recherche autour des individus déjà performants (augmente l'aspect exploitation de l'algorithme).
L’impact de cette différence se traduit à différentes échelles:
On peut néanmoins remarquer que les 2 algorithmes convergent vers la valeur optimale avec les paramètres choisis.
Comme mentionné précédemment, la sélectivité de l'algorithme influe sur la vitesse de convergence et aussi sur la façon dont l'algorithme explore l'environnement. On peut ici voir l'impact sur ces 2 éléments. En revanche, le 3ème aspect, la qualité de l'optimum n'est pas visible ici. Mais dans l'ensemble, en particulier quand l'espace de solution est plus large / complexe, il devient intéressant d'avoir une algorithme qui offre une population moins homogène. En effet, il est possible qu'en croisant 2 individus peu performants on obtienne 1 individu très performant.
Par exemple : si on prend 2 voitures, une voiture très aérodynamique avec un mauvais moteur, et une voiture peu aérodynamique avec un excellent moteur et que l'on cherche à obtenir la meilleur voiture possible, ces 2 cas sont peu performants et devraient donc être éliminés. Pour autant, si on prend l’aérodynamisme de la première et le moteur de la seconde on obtient quelque chose de très performant.
Autrement dit, en particulier en grande dimension, vouloir sélectionner uniquement les individus les plus performants sur des considérations globales (la fitness) peut avoir un effet négatif parce qu'une partie de l'information d'un individu peut lui permettre d'être optimisé localement. Conserver une population plus disparate augmente la chance de conserver de tels individus.
Si on observe les différentes courbes ci-dessus on peut observer différentes situations. Pour les populations qui sont plutôt larges, la convergence est atteinte assez rapidement (<50 générations) et les générations >50 sont dès lors inutiles, le maximum ayant été trouvé. A l’inverse, dans certains cas, en particulier pour des populations de taille plus réduite, on peut observer des sauts d’optimum après des périodes de stagnation parfois longue (>80 générations). Comment dès lors optimiser le nombre de générations à réaliser par l’algorithme ?
On peut choisir 2 critères pour évaluer la dispersion de la population : se baser sur la fitness. se baser sur la représentation.
Si on s’intéresse à l’algorithme 3 pour 50 individus on peut observer que les 2 critères ne donnent pas forcément les mêmes résultats.
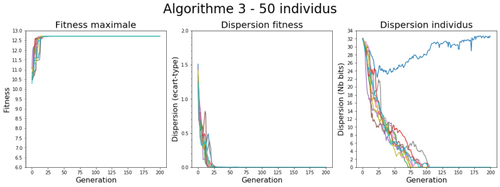
Si la convergence de la fitness coïncide naturellement avec une dispersion plus faible de la population sur ce paramètre, on peut en revanche noter que la population n’a en pratique pas encore complètement convergé, on est ici dans une représentation génotypique et on peut voir qu’après 25 générations, on trouve en moyenne encore 15 bits de différences entre les individus. Certains effets de bord liés à la représentation sont aussi visibles (courbe bleue). L’optimum (0,0) se trouvant entre 2 représentations possibles (à cause de l’échantillonnage). Dans notre cas on va donc avoir plusieurs sous-populations qui vont se créer avec des sous représentations un peu au-dessus et un peu en-dessous de 0. Le nombre de bits différent d’un individu à l’autre qui peut être important est dû à la représentation génotypique: en binaire, une variation faible de la valeur peut se traduire par des différences importantes au sein de la représentation. Par exemple en binaire : 3 -> [011] mais 4->[100] Une des solutions à ce type de problème est d’utiliser par exemple un code gray qui permet que 2 nombres proches aient des représentations proches.
Pour résumer, il peut être intéressant de chercher à arrêter l’algorithme quand la population converge vers un point donné mais il faut être en mesure de prendre des précautions. En effet, il n’y a pas de corrélation directe entre la vitesse de convergence de la population et celle de la fitness, voire certaines situations où la population ne converge pas du tout ou très lentement (voir ci-dessous avec l’algorithme 2). Comme on peut le voir sur l’algorithme 2, on ne peut pas toujours se baser sur ces méthodes pour obtenir un critère d’arrêt pertinent.
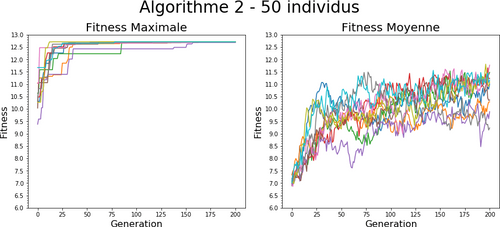
Ici, l'optimum global est trouvé, mais la population en moyenne est beaucoup plus dispersée que sur les autres algorithmes et ne converge donc pas même une fois le maximum trouvé.
Les articles d'OpenAi et UberAi mettaient en avant la robustesse des algorithmes évolutionnistes au paramétrage. On peut effet en faisant varier les paramètres observer une inertie assez importante de l'algorithme vis-à-vis de ses paramètres de configuration. Dans le cas de l'algorithme 3 : taille de la population, taux de croisement et taux de mutation.
Ci-dessous, les courbes pour 10 itérations de l'algorithme avec un taux de croisement de 50%, de mutation de 0.1 et une population de 20 individus. Comparativement aux courbes de l'algorithmes 3 montrées plus haut (pour 50 individus, un taux de croisement de 0.2 et un taux de mutation de 0.01) on peut observer que la convergence est légèrement plus faible mais reste acceptable.
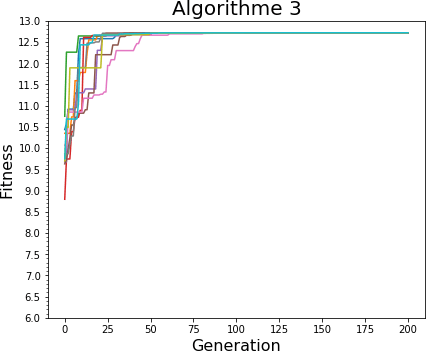
Il faut toutefois prendre la stabilité des paramètres avec la conscience des limites qui l'entourent, par exemple dans le cas de l'algorithme 1, passer l'écart-type de la perturbation normale de 1 à 5, diminue de façon très importante la vitesse de convergence de l'algorithme. Ainsi, la "plage de stabilité" de l'algorithme dépend fortement du problème et de l'algorithme. Toutefois, de petite variations, tout comme les valeurs d'initialisation, ont un impact assez limité sur la convergence de l'algorithme.
L'algorithme 1 diffère des 2 autres par le choix de sa représentation. Les algorithmes 2 et 3 utilisent une représentation génotypique en représentant chaque individu comme une séquence de 64 bits, x et y étant chacun définis sur 32 bits. L'algorithme 1 utilise lui une représentation phénotypique des individus, à savoir un vecteur (x,y) de 2 nombres réels.
En pratique sur cet exemple, on n'observe assez peu de différences au niveau du résultat final entre les représentation phénotypique et génotypique et les vitesses de convergences sont sensiblement identiques pour la fitness maximale. Cette observation n'est toutefois pas généralisable à tous les problèmes, les choix de représentation pouvant avoir un impact important sur les résultats et la progression de l'algorithme.

La première partie était consacrée à la découverte de la structure des algorithmes évolutionnistes ainsi qu'à leurs différents éléments constitutifs. Cette seconde partie s'intéressait aux performances des algorithmes évolutionnistes et à l'impact et l'importance du paramétrage. La nature des problèmes d'optimisation fait qu'il est impossible de savoir quel algorithme sera le plus performant sur un problème donné. D'autant plus que le choix des paramètres peut influer sur la performance de l'algorithme sur le problème. Néanmoins, les algorithmes évolutionnistes offrent plusieurs outils pour permettre d'avoir une performance qui soit la plus optimale possible. En particulier, ils offrent des moyens pour gérer le dilemme exploration / exploitation qui conditionne la vitesse et la qualité du résultat obtenu, et offrent des garanties au niveau de leur convergence en étant assez robustes à des variations de valeur des paramètres. Empiriquement, les algorithmes évolutionnistes sont particulièrement intéressants sur des problèmes à grande dimension ou quand l’espace solution est peu connu. A l’inverse, le fait qu’ils n’exploitent pas les informations préalable sur la nature de l’espace les rend potentiellement moins intéressants que d’autres types d’algorithmes dans ces situations. On peut aussi apprécier le paramétrage très limpide des algorithmes évolutionnistes qui est de 2 types et assez simple à mettre en oeuvre par la robustesse des algorithmes : - le choix d'algorithmes (sélection, mutation et croisement), de la représentation ainsi que de la fonction de fitness. - le choix des paramètres de ces algorithmes (probabilité de croisement, mutation), la taille de la population et le nombre de générations.